题目内容
【题目】如图,某公司租用两种型号的货车各一辆,分別将产品运往甲市与乙市(运费收费标准如下表),已知该公司到乙市的距离比到甲市的距离远30km,B车的总运费比A车的总运费少1080元.
(1)求这家公司分别到甲、乙两市的距离;
(2)若A,B两车同时从公司出发,其中B车以60km/h的速度匀速驶向乙市,而A车根据路况需要,先以45kmh的速度行驶了3小吋,再以75km/h的速度行驹到达甲市.
①在行驶的途中,经过多少时间,A,B两车到各自目的地的距离正好相等?
②若公司希望B车能与A车同吋到达目的地,B车必须在以60km/h的速度行驶一段时间后提速,若提速后的速度为70km/h(速度从60km/h提速到70km/h的时间忽略不汁),则B车应该在行驶 小时后提速.

【答案】(1)该公司距离甲市270千米,距离乙市300千米;(2)①经过2小时或4小时,A、B两车到各自目的地的距离相等;②3.6.
【解析】
(1)设该公司距离甲市千米,根据“该公司到乙市的距离比到甲市的距离远30km,”得该公司到乙市的距离为(x+30)千米,根据“B车的总运费比A车的总运费少1080元”列方程求解即可;
(2)①设在行驶的途中,经过a(h),A、B两车到各自目的地的距离正好相等,a分0<a≤3和a>3两种情况列一元一次方程求解即可;
②先计算出A车到达甲市的时间为4.8h,再根据B车“行驶两段路程之和=300”列出方程求解即可.
(1)设该公司距离甲市x千米根据题意得:
24x-1080=18(x+30)
解得:x=270,
∴x+30=270+30=300
答:该公司距离甲市270千米,距离乙市300千米.
(2)①设在行驶的途中,经过a(h),A、B两车到各自目的地的距离正好相等,
根据题意,得
当0<a≤3时,270-45a=300-60a,
解得:a=2;
a>3时,270-45x3-75(a-3)=300-60a,
解得:a=4,
答:在行驶的途中,经过2h或4h,A、B两车到各自目的地的距离正好相等;
②由题意可知:A车到达甲市的时间为![]() ,
,
设B车应该在行驶t(h)后提速,根据题意可得
60t+70(4.8-t)=300,
解方程,得t=3.6,
即若公司希望B车能与A车同时到达目的地,则B车应该在行驶3.6h后提速.
故答案为:3.6.

【题目】如图所示的表格是某次篮球联赛部分球队的积分表,则下列说法不正确的是( )
队名 | 比赛场数 | 胜场 | 负场 | 积分 |
前进 | 14 | 10 | 4 | 24 |
光明 | 14 | 9 | 5 | 23 |
远大 | 14 | 7 | a | 21 |
卫星 | 14 | 4 | 10 | b |
钢铁 | 14 | 0 | 14 | 14 |
… | … | … | … | … |
A.负一场积1分,胜一场积2分B.卫星队总积分b=18
C.远大队负场数a=7D.某队的胜场总积分可以等于它的负场总积分
【题目】为贯彻落实云南省教育厅提出的“三生教育”,在母亲节来临之际,某校团委组织了以“珍爱生命,学会生存,感恩父母”为主题的教育活动,在学校随机调查了50名同学平均每周在家做家务的时间,统计并制作了如下的频数分布和扇形统计图:
组别 | 做家务的时间 | 频数 | 频率 |
A | 1≤t<2 | 3 | 0.06 |
B | 2≤t<4 | 20 | 0.40 |
C | 4≤t<6 | A | 0.30 |
D | 6≤t<8 | 8 | B |
E | t≥8 | 4 | 0.08 |
根据上述信息回答下列问题: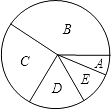
(1)a= , b=;
(2)在扇形统计图中,B组所占圆心角的度数为;
(3)全校共有2000名学生,估计该校平均每周做家务时间不少于4小时的学生约有多少人?