Question

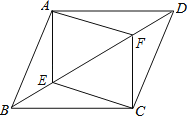
【题目】已知平行四边形ABCD，连接AF，CE、AF平分交BC于点F，CE平分交AD于点E．

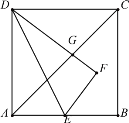
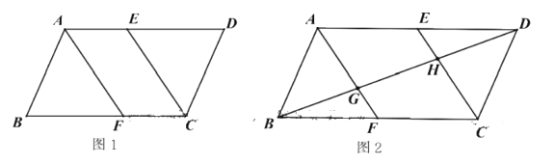
（1）如图1，求证：四边形AFCE为平行四边形；

（2）如图2，连接BD，分别交AF、CE于G、H，若，在不添加其他辅助线的情况下，直接找出图中面积为平行四边形ABCD面积的的三角形或四边形．

Answer 1

【答案】（1）详见解析；（2），；四边形，四边形

【解析】

（1）利用角平分线的性质再结合平行四边形的性质进而得出AF∥EC，即可得出答案；

（2）连接EF，证明E、F分别为AD和BC中点，即可根据三角形面积公式和平行四边形面积公式，知和面积为行四边形ABCD面积的；再根据图形的对称性，可知四边形和四边形面积相等，即可得出答案．

证明：（1）∵AF平分∠BAD，CE平分∠BCD，

∴∠FAE=∠BAE，∠FCE=∠FCD，

∵四边形ABCD是平行四边形，

∴∠BAE=∠FCD，AD∥BC，

∴∠FAE=∠FCE，∠FCE=∠CED，

∴∠FAE=∠CED，

∴AF∥EC，

又∵AE∥CF，

∴四边形AFCE为平行四边形；

（2）如图，连接EF,

∵AF平分，

∴∠EAF=∠BAF，

∵四边形ABCD为平行四边形，

∴AD∥BC，

∴∠EAF=∠BFA，

∴∠BAF=∠BFA，

∴BA=BF，

∵，

∴BF=FC，即点F为BC的中点，

同理可证点E为AD中点，

∴，

易证四边形，四边形为全等图形，

∴，

∴面积为平行四边形ABCD面积的的三角形或四边形有：，，四边形，四边形．