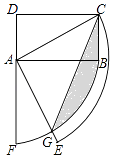��Ŀ����
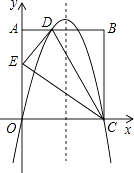
����Ŀ����ͼ���ھ���OABC�У�AO=10��AB=8����ֱ��CD�۵�����OABC��һ��BC��ʹ��B����OA���ϵĵ�E�����ֱ���OC��OA���ڵ�ֱ��Ϊx�ᣬy�Ὠ��ƽ��ֱ������ϵ��������y=ax2+bx+c����O��D��C���㣮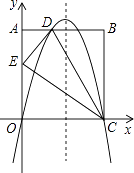
��1����AD�ij��������ߵĽ���ʽ��
��2��һ����P�ӵ�E��������EC��ÿ��2����λ�����ٶ����C�˶���ͬʱ����Q�ӵ�C��������CO��ÿ��1����λ�����ٶ����O�˶�������P�˶�����Cʱ������ͬʱֹͣ�˶������˶�ʱ��Ϊt�룬��tΪ��ֵʱ����P��Q��CΪ��������������ADE���ƣ�
��3����N�������߶Գ����ϣ���M���������ϣ��Ƿ���������ĵ�M���N��ʹ��M��N��C��EΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д����M���N�����꣨��д�����̣����������ڣ���˵�����ɣ�
���𰸡�
��1���⣺���ı���ABCOΪ���Σ�
���OAB=��AOC=��B=90�㣬AB=CO=8��AO=BC=10��
�����⣬��BDC�ա�EDC��
���B=��DEC=90�㣬EC=BC=10��ED=BD��
�ɹ��ɶ�����EO=6��
��AE=10��6=4��
��AD=x����BD=ED=8��x���ɹ��ɶ�������x2+42=��8��x��2��
��ã�x=3����AD=3��
��������y=ax2+bx+c����D��3��10����C��8��0����O��0��0��
�� ![]() ��
��
��� 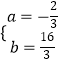
�������ߵĽ���ʽΪ��y=�� ![]() x2+
x2+ ![]() x
x
��2���⣺����һ���ߡ�DEA+��OEC=90�㣬��OCE+��OEC=90�㣬
���DEA=��OCE��
�ɣ�1���ɵ�AD=3��AE=4��DE=5��
��CQ=t��EP=2t����PC=10��2t��
����PQC=��DAE=90�㣬��ADE�ס�QPC��
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() ��
��
���t= ![]() ��
��
����QPC=��DAE=90�㣬��ADE�ס�PQC��
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() ��
��
���t= ![]() ��
��
�൱t= ![]() ��
�� ![]() ʱ����P��Q��CΪ��������������ADE����
ʱ����P��Q��CΪ��������������ADE����
����������E��0��6����C��8��0����
��lEC��y=�� ![]() x+6��
x+6��
�� ![]() ��EP=2t��
��EP=2t��
��Px= ![]() t��
t��
��P�� ![]() t����
t���� ![]() t+6����Q��8��t��0����
t+6����Q��8��t��0����
�ߡ�PQC�ס�ADE���ҡ�ECO=��AED��
��PQ��OC��PQ��PC��
��PQ��OCʱ��Px=Qx���� ![]() t=8��t����t1=
t=8��t����t1= ![]() ��
��
��PQ��PCʱ��KPQKPC=��1����t2= ![]()
��3���⣺����һ��������ڷ���������M��N�㣬������������ۣ�
�� 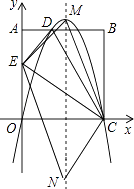
ECΪƽ���ı��εĶԽ��ߣ����������ߵĶԳ��ᾭ��EC�е㣬���ı���MENC��ƽ���ı��Σ���ôM���Ϊ�����߶��㣻
��M��4�� ![]() ������ƽ���ı��εĶԽ�����ƽ�֣���ô�߶�MN�ر�EC�е㣨4��3��ƽ�֣���N��4����
������ƽ���ı��εĶԽ�����ƽ�֣���ô�߶�MN�ر�EC�е㣨4��3��ƽ�֣���N��4���� ![]() ����
����
��ECΪƽ���ı��εıߣ���EC ![]() MN����N��4��m������M��4��8��m+6����M��4+8��m��6����
MN����N��4��m������M��4��8��m+6����M��4+8��m��6����
��M����4��m+6�����������ߵĽ���ʽ�У��ã�m=��38����ʱ N��4����38����M����4����32����
��M��12��m��6�����������ߵĽ���ʽ�У��ã�m=��26����ʱ N��4����26����M��12����32����
���ϣ����ڷ���������M��N�㣬�����ǵ�����Ϊ��
��M1����4����32����N1��4����38������M2��12����32����N2��4����26������M3��4�� ![]() ����N3��4����
����N3��4���� ![]() ��
��
��������M��N��C��EΪ������ı�����ƽ���ı��Σ���N��4��t����C��8��0����E��0��6����
�� ![]() ��
��
��M1��4��6��t����ͬ��M2����4��t+6����M3��12��t��6����
�ੁ ![]() t����t=��
t����t=�� ![]() ��
��
�� ![]() ������4��2+
������4��2+ ![]() ����4��=t+6����t=��38��
����4��=t+6����t=��38��
�� ![]() ��122+
��122+ ![]() ��12=t��6����t=��26��
��12=t��6����t=��26��
���ϣ����ڷ���������M��N�㣬�����ǵ�����Ϊ��
��M1��4�� ![]() ����N1��4����
����N1��4���� ![]() ������M2��12����32����N2��4����26����
������M2��12����32����N2��4����26����
��M3����4����32����N3��4����38����
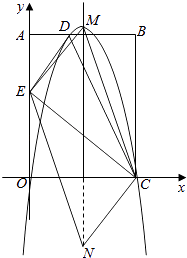
����������1�������۵�ͼ�ε���Գ��ԣ���CED����CBDȫ�ȣ�������Rt��CEO�����OE�ij��������ɵõ�AE�ij�����Rt��AED�У�AD=AB��BD��ED=BD�����ù��ɶ��������AD�ij�����һ����ȷ��D�����꣬���ô���ϵ����������������ߵĽ���ʽ����2�����ڡ�DEC=90�㣬������ȷ�����ǡ�AED=��OCE������P��Q��CΪ��������������ADE���ƣ���ô��QPC=90����PQC=90�㣬Ȼ��������������£��ֱ��������������εĶ�Ӧ�߳ɱ��������Ӧ��t��ֵ����3��������M��N��C��EΪ������ı��Σ��ߺͶԽ��߶�û��ȷָ��������Ҫ������������ۣ���EC��ƽ���ı��εĶԽ��ߣ���ôEC��MN�ػ���ƽ�֣�����EC���е������������߶Գ����ϣ�����M��һ���������ߵĶ��㣻��EC��ƽ���ı��εıߣ���ôEC��MNƽ������ȣ����������N�����꣬Ȼ����E��C�ĺᡢ��������ʾ��M�����꣬�ٽ���M���������ߵĽ���ʽ�У�����ȷ��M��N�����꣮