Question

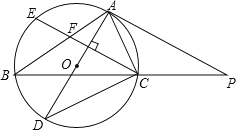
【题目】如图，AD是△ABC的外接圆⊙O的直径，点P在BC延长线上，PA是⊙O的切线，且∠B=35°．

（1）求∠PAC的度数．

（2）弦CE⊥AD交AB于点F，若AFAB=12，求AC的长．

Answer 1

【答案】（1）35°；（2）．

【解析】

（1）根据直径得出∠ACD=90°，根据切线的性质得出∠PAD=90°，进而得到∠PAC=∠D，结合同弧的性质即可得出答案；

（2）根据垂径定理得出，进而证出Rt△AFC∽Rt△ACB得到，即可得出答案.

解：（1）∵AD⊙O的直径，

∴∠ACD=90°，

∴∠D=90°﹣∠CAD．

∵PA是圆O的切线，

∴AP⊥AD，

∴∠PAD=90°，

∴∠PAC=90°﹣∠CAD，

∴∠PAC=∠D．

∵∠D=∠B，

∴∠PAC=∠B=35°；

（2）∵CF⊥AD，

∴，

∴∠ACE=∠ABC，

∴Rt△AFC∽Rt△ACB，

∴，

∴AC2=AFAB=12，

∴AC=2．