题目内容
【题目】直角梯形的一个内角为
，较长的腰为6
，一底为5，则这个梯形的面积为（ ）
A. 
B. 
C. 25
D. 或
【答案】D
【解析】试题分析：根据“直角梯形的一个内角为120°，较长的腰为6cm”可求得直角梯形的高，由于一底边长为5cm不能确定是上底还是下底，故要分两种情况讨论梯形的面积，根据梯形的面积公式=
（上底+下底）×高，分别计算即可．
解：根据题意可作出下图.
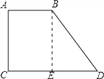
BE为高线,BE⊥CD,即∠A=∠C=90°,∠ABD=120°，BD=6cm，
∵AB∥CD,∠ABD=120°，
∴∠D=60°，
∴BE=6×sin60°=3
cm; ED=6×cos60°=3cm；
当AB=5cm时,CD=5+3=8cm,梯形的面积=
cm2；
当CD=5cm时,AB=53=2cm,梯形的面积=
cm2；
故梯形的面积为
或
，
故选D.
练习册系列答案
相关题目
【题目】某校共有1000名学生，为了了解他们的视力情况，随机抽查了部分学生的视力，并将调查的数据整理绘制成直方图和扇形图.
（1）这次共调查了多少名学生？扇形图中的a、b值分别是多少？
（2）补全频数分布直方图；
（3）在光线较暗的环境下学习的学生占对应被调查学生的比例如下表：
视力 | ≤0.35 | 0.35～0.65 | 0.65～0.95 | 0.95～1.25 | 1.25～1.55 |
比例 |
|
|
|
|
|
根据调查结果估计该校有多少学生在光线较暗的环境下学习？
