题目内容
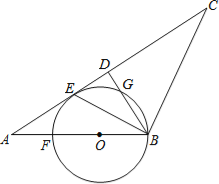
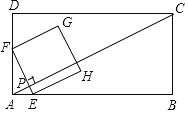
【题目】如图,在平面直角坐标系![]() 中,以
中,以![]() 为圆心作⊙
为圆心作⊙![]() ,⊙
,⊙![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() 为⊙
为⊙![]() 上不同于
上不同于![]() 、
、![]() 的任意一点,连接
的任意一点,连接![]() 、
、![]() ,过
,过![]() 点分别作
点分别作![]() 于
于![]() ,
,![]() 于
于![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,
,![]() .当
.当![]() 点在⊙
点在⊙![]() 上顺时针从点
上顺时针从点![]() 运动到点
运动到点![]() 的过程中,下列图象中能表示
的过程中,下列图象中能表示![]() 与
与![]() 的函数关系的部分图象是( )
的函数关系的部分图象是( )

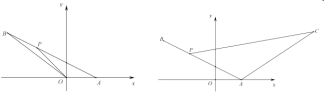
A.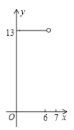 B.
B.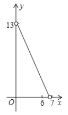 C.
C.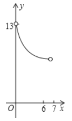 D.
D.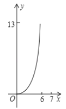
【答案】A
【解析】
由题意,连接PC、EF,利用勾股定理求出![]() ,然后得到AB的长度,由垂径定理可得,点E是AQ中点,点F是BQ的中点,则EF是△QAB的中位线,即
,然后得到AB的长度,由垂径定理可得,点E是AQ中点,点F是BQ的中点,则EF是△QAB的中位线,即![]() 为定值,由
为定值,由![]() ,即可得到答案.
,即可得到答案.
解:如图,连接PC,EF,则
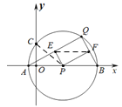
∵点P为(3,0),点C为(0,2),
∴![]() ,
,
∴半径![]() ,
,
∴![]() ;
;
∵![]() 于
于![]() ,
,![]() 于
于![]() ,
,
∴点E是AQ中点,点F是BQ的中点,
∴EF是△QAB的中位线,
∴![]() 为定值;
为定值;
∵AB为直径,则∠AQB=90°,
∴四边形PFQE是矩形,
∴![]() ,为定值;
,为定值;
∴当![]() 点在⊙
点在⊙![]() 上顺时针从点
上顺时针从点![]() 运动到点
运动到点![]() 的过程中,y的值不变;
的过程中,y的值不变;
故选:A.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目