题目内容
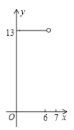
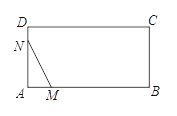
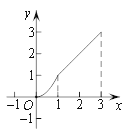
【题目】如图1,在平面直角坐标系![]() 中,点
中,点![]() ,点
,点![]() .
.
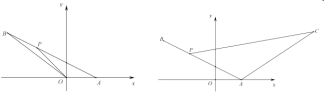
(1)求直线![]() 的函数表达式;
的函数表达式;
(2)点![]() 是线段
是线段![]() 上的一点,当
上的一点,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
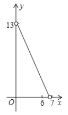
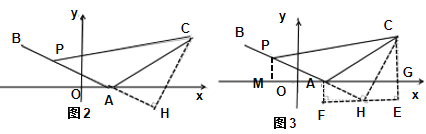
(3)如图2,在(2)的条件下,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 落在点
落在点![]() 处,连结
处,连结![]() ,求
,求![]() 的面积,并直接写出点
的面积,并直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,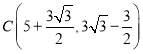 .
.
【解析】
(1)利用待定系数法即可解决问题;
(2)过点![]() 、
、![]() 分别做
分别做![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,根据相似三角形的性质得出PM的长,即点P的纵坐标,代入直线解析式,从而求解;
,根据相似三角形的性质得出PM的长,即点P的纵坐标,代入直线解析式,从而求解;
(3)过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,若求
,若求![]() 的面积,求出CH的长即可,根据旋转120°,得∠CAH=60°,解直角三角形AHC即可得出CH长,从而求解,
的面积,求出CH的长即可,根据旋转120°,得∠CAH=60°,解直角三角形AHC即可得出CH长,从而求解,
解:(1) )∵A(2,0),![]() ,
,
设直线AB的解析式为y=kx+b,则有![]() ,
,
解得:![]() ,
,
∴直线AB的解析式为![]() .
.
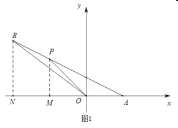
(2)如图1,过点![]() 、
、![]() 分别做
分别做![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,即PM∥BN.
,即PM∥BN.
∵![]() ,
,
∴AP:AB=2:3,
∴![]() =
=![]()
∴![]()
将![]() 代入解析式
代入解析式![]() 可得
可得
![]() ,∴
,∴![]()
(3)①如图2,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
∵![]() 中,由勾股定理得:AP=
中,由勾股定理得:AP=![]() ,
,
在![]() 中,
中,![]() ,
,![]()
∴![]()
∴![]() ;
;
②过点H作FE∥x轴,过点C作CE⊥FE于点E,交x轴于点G,过点A作AF⊥FE于点F,
Rt△ACH中, AH=![]() ,
,
∵PM∥AF,AM∥HF,根据直角相等、两直线平行,同位角相等易证△APM∽△HAF,AP=2![]() ,AM=4,PM=2,
,AM=4,PM=2,
∴![]() ,即
,即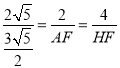 ,
,
解得:AF=![]() ,HF=3,
,HF=3,
∵∠AHF+∠CHE=∠AHF +∠FAH=90°,
∴∠CHE=∠FAH,
∵∠HEC=∠AFH=90°,
∴△HEC∽△AFH,
方法同上得:CE=3![]() ,HE=
,HE=![]() ,
,
由四边形AFEG是矩形,得AF=GE= ![]() ,AG=FH+HE,
,AG=FH+HE,
∴OG=OA+ FH+HE=2+3+![]() =5+
=5+![]() ,CG=CE-EG=3
,CG=CE-EG=3![]() -
-![]() ,
,
即点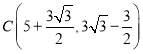 .
.

【题目】为了了解某小区青年对“高铁”、“扫码支付”、“网购”和“共享单车”新四大发明的喜爱程度,随机调查该小区一部分青年(每名青年只能选一个),并将调查结果制成如图所示统计表与条形统计图.
青年最喜爱的新四大发明人数统计表
节目 | 人数(名) | 百分比 |
共享单车 | 5 |
|
扫码支付 | 15 |
|
网购 |
|
|
高铁 | 10 |
|
青年最喜爱的新四大发明人数条形统计图
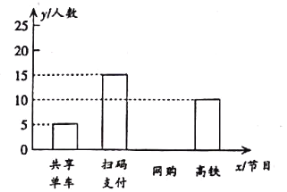
(1)计算![]() 的值
的值![]() ;
;
(2)请补全条形统计图;
(3)在被调查喜爱“共享单车”青年中,小明一周内使用共享单车的次数分别为:1,3,5,12,![]() ,若整数
,若整数![]() 是这组数据的中位数,直接写出该组数据的平均数.
是这组数据的中位数,直接写出该组数据的平均数.