题目内容
【题目】在Rt![]() 中,∠A=90°,AC=4,
中,∠A=90°,AC=4,![]() ,将
,将![]() 沿着斜边BC翻折,点A落在点
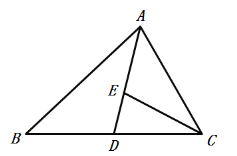
沿着斜边BC翻折,点A落在点![]() 处,点D、E分别为边AC、BC的中点,联结DE并延长交
处,点D、E分别为边AC、BC的中点,联结DE并延长交![]() 所在直线于点F,联结
所在直线于点F,联结![]() ,如果
,如果![]() 为直角三角形时,那么
为直角三角形时,那么![]() ____________
____________
【答案】4或![]()
【解析】
当△A1EF为直角三角形时,存在两种情况:
①当∠A1EF=90°时,如图1,根据对称的性质和平行线可得:A1C= A1E=4,根据直角三角形斜边中线的性质得:BC=2 A1E=8,最后利用勾股定理可得AB的长;
②当∠A1FE=90°时,如图2,证明△ABC是等腰直角三角形,可得AB=AC=4.
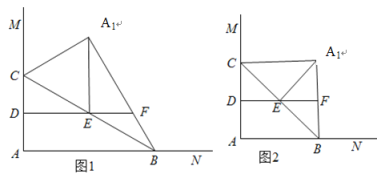
解:当△A1EF为直角三角形时,存在两种情况:
①当∠A1EF=90°时,如图1,
∵△A1BC与△ABC关于BC所在直线对称,
∴A1C=AC=4,∠ACB=∠A1CB,
∵点D,E分别为AC,BC的中点,
∴D、E是△ABC的中位线,
∴DE∥AB,
∴∠CDE=∠MAN=90°,
∴∠CDE=∠A1EF,
∴AC∥A1E,
∴∠ACB=∠A1EC,
∴∠A1CB=∠A1EC,
∴A1C= A1E=4,
Rt△A1CB中,∵E是斜边BC的中点,
∴BC=2 A1E=8,
由勾股定理得:AB2=BC2-AC2,
∴AB=![]()
②当∠A1FE=90°时,如图2,
∵∠ADF=∠A=∠DFB=90°,
∴∠ABF=90°,
∵△A1BC与△ABC关于BC所在直线对称,
∴∠ABC=∠CB A1=45°,
∴△ABC是等腰直角三角形,
∴AB=AC=4;
综上所述,AB的长为4![]() 或4;
或4;
故答案为:4![]() 或4.
或4.

练习册系列答案
相关题目