题目内容
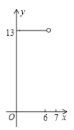
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)过点![]() 作与
作与![]() 轴平行的直线,交抛物线于点
轴平行的直线,交抛物线于点![]() ,
,![]() .当
.当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 的取值范围为
的取值范围为![]() 或
或![]() .
.
【解析】
(1)先求出抛物线的对称轴,利用对称性求出A、B的坐标,然后把点代入抛物线,即可求出m的值;
(2)根据根的判别式得到m的范围,再结合![]() ,然后分为:①开口向上,②开口向下,两种情况进行分析,即可得到答案.
,然后分为:①开口向上,②开口向下,两种情况进行分析,即可得到答案.
解:(1)抛物线对称轴为直线![]() .
.
∴点![]() 关于直线
关于直线![]() 对称,
对称,
∵![]()
![]() 抛物线与
抛物线与![]() 轴交于点
轴交于点![]() ,
,
将![]() 代入
代入![]() 中,
中,
得![]() ,
,
∴![]() ;
;
(2)抛物线![]() 与
与![]() 轴有两个交点
轴有两个交点
∴![]() ,即
,即![]() ,
,
解得:![]() 或
或![]() ;
;
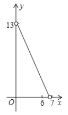
①若![]() ,开口向上,如图,
,开口向上,如图,
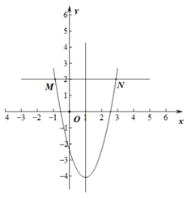
当![]() 时,有
时,有![]() ,
,
解得:![]() ;
;
∵![]() 或
或![]() ,
,
∴![]() ;
;
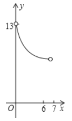
②若![]() ,开口向下,如图,
,开口向下,如图,
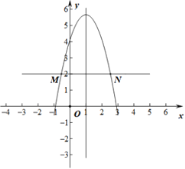
当![]() 时,有
时,有![]() ,
,
解得:![]() ,
,
∵![]() 或
或![]() ,
,
∴![]() ;
;
综上所述,![]() 的取值范围为:
的取值范围为:![]() 或
或![]() .
.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目