题目内容
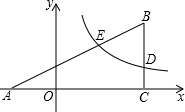
如图,在平面直角坐标系xOy中,△ABC的边AC在x轴上,边BC⊥x轴,双曲线y=
(x>0)与边BC交于点D(4,m),与边AB交于点E(2,n).
(1)求n关于m的函数关系式;
(2)若BD=2,tan∠BAC=
,求k的值和点B的坐标.
| k |
| x |
(1)求n关于m的函数关系式;
(2)若BD=2,tan∠BAC=
| 1 |
| 2 |

(1)∵点D(4,m),点E(2,n)在双曲线y=
(x>0)上,
∴4m=2n,解得n=2m;
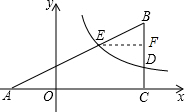
(2)过点E作EF⊥BC于点F,
∵由(1)可知n=2m,
∴DF=m,
∵BD=2,
∴BF=2-m,
∵点D(4,m),点E(2,n),
∴EF=4-2=2,
∵EF∥x轴,
∴tan∠BAC=tan∠BEF=
=
=
,解得m=1,
∴D(4,1),
∴k=4×1=4,B(4,3).
| k |
| x |
∴4m=2n,解得n=2m;
(2)过点E作EF⊥BC于点F,
∵由(1)可知n=2m,
∴DF=m,
∵BD=2,
∴BF=2-m,
∵点D(4,m),点E(2,n),
∴EF=4-2=2,
∵EF∥x轴,
∴tan∠BAC=tan∠BEF=
| BF |
| EF |
| 2-m |
| 2 |
| 1 |
| 2 |
∴D(4,1),
∴k=4×1=4,B(4,3).


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目