题目内容
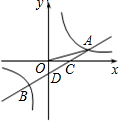
如图1,在平面直角坐标系中,等腰Rt△AOB的斜边OB在x轴上,直线y=3x-4经过等腰Rt△AOB的直角顶点A,交y轴于C点,双曲线y=
也经过A点.
(1)求点A坐标;
(2)求k的值;
(3)若点P为x正半轴上一动点,在点A的右侧的双曲线上是否存在一点M,使得△PAM是以点A为直角顶点的等腰直角三角形?若存在,求出点M的坐标;若不存在,请说明理由.
(4)若点P为x负半轴上一动点,在点A的左侧的双曲线上是否存在一点N,使得△PAN是以点A为直角顶点的等腰直角三角形?若存在,求出点N的坐标;若不存在,请说明理由.

| k |
| x |
(1)求点A坐标;
(2)求k的值;
(3)若点P为x正半轴上一动点,在点A的右侧的双曲线上是否存在一点M,使得△PAM是以点A为直角顶点的等腰直角三角形?若存在,求出点M的坐标;若不存在,请说明理由.
(4)若点P为x负半轴上一动点,在点A的左侧的双曲线上是否存在一点N,使得△PAN是以点A为直角顶点的等腰直角三角形?若存在,求出点N的坐标;若不存在,请说明理由.

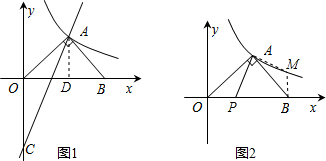
(1)作AD⊥x轴于D
∵△AOB为等腰直角三角形
∴OD=AD=BD
设A(a,a),
则a=3a-4,
解得a=2
∴点A(2,2);
(2)又点A在y=
上,
∴k=4,反比列函数为y=
;
(3)存在.
设M(m,n)
∵∠PAM=∠OAB=90°
∴∠OAP=∠BAM
∵OA=ABAP=AM
∴△OAP≌△BAM
∴∠ABM=∠AOP=45°
∴∠OBM=90°,即MB⊥x轴
∵△ABO是等腰直角三角形,A(2,2)
∴OB=4
∵点M在y=
上
∴M(4,1);
(4)不存在
由(3)中所证易知:
假设在双曲线上存在点N,
若△PAN为等腰直角三角形
则:△PAB≌△NAO
∴∠NOA=∠PBA=45°
∴∠NOB=90°
则点N在y轴上,
∴点N不在双曲线上
∴点N不存在.
∵△AOB为等腰直角三角形
∴OD=AD=BD
设A(a,a),
则a=3a-4,
解得a=2
∴点A(2,2);
(2)又点A在y=
| k |
| x |
∴k=4,反比列函数为y=
| 4 |
| x |
(3)存在.
设M(m,n)
∵∠PAM=∠OAB=90°
∴∠OAP=∠BAM
∵OA=ABAP=AM
∴△OAP≌△BAM
∴∠ABM=∠AOP=45°
∴∠OBM=90°,即MB⊥x轴
∵△ABO是等腰直角三角形,A(2,2)
∴OB=4
∵点M在y=
| 4 |
| x |
∴M(4,1);
(4)不存在
由(3)中所证易知:
假设在双曲线上存在点N,
若△PAN为等腰直角三角形
则:△PAB≌△NAO
∴∠NOA=∠PBA=45°
∴∠NOB=90°
则点N在y轴上,
∴点N不在双曲线上
∴点N不存在.


练习册系列答案
相关题目
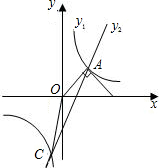 A点,一次函数y2=ax-b的图象过A点且与反比例函数图象的另一交点为C(-1,m),连接OC
A点,一次函数y2=ax-b的图象过A点且与反比例函数图象的另一交点为C(-1,m),连接OC