题目内容
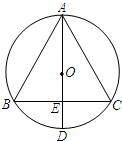
等腰△ABC中,AB=AC,高AD交对边BC于D,P为AD上任意一点.以P为圆心过B、C两点的圆交直线AB、AC于G、F两点,证明:BG=CF.
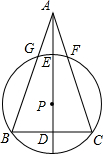

证明:连接GF交AD于H.
则∠AGF=∠C,∠AFG=∠B,
∵AB=AC,
∴∠B=∠C,
∴∠AGF=∠AFG,
∴AG=AF,
∴BG=CF.

则∠AGF=∠C,∠AFG=∠B,
∵AB=AC,
∴∠B=∠C,
∴∠AGF=∠AFG,
∴AG=AF,
∴BG=CF.


练习册系列答案
相关题目