��Ŀ����
����Ŀ����֪�߶�MN=8��C���߶�MN��һ���㣬��MN��ͬ��ֱ����ȱߡ�CMD�͵ȱߡ�CNE��
��1����ͼ�٣�����DN��EM�������߶��ཻ�ڵ�H����֤ME=DN�������DHM�Ķ�����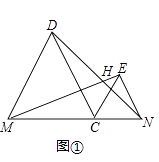
��2����ͼ�ڣ�����D��E�ֱ����߶�MN�Ĵ��ߣ�����ֱ�ΪF��G���ʣ��ڵ�C�˶������У�DF+EG�ij����Ƿ�Ϊ��ֵ������ǣ�����������ֵ�����������˵�����ɣ�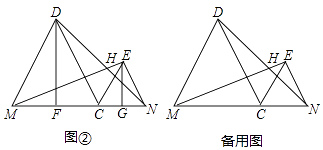
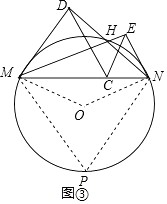
��3������C�ɵ�M�Ƶ���Nʱ����H�Ƶ���·������Ϊ��ֱ��д�������
���𰸡�
��1��
֤�����ߡ�CMD���CNE�ǵȱ������Σ�
��CM=CD��EC=NC����DCM=��ECN=60�㣬
���DCN=��MCE=120�㣬
�ڡ�MCE���DCN�У� 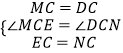 ��
��
���MCE�ա�DCN��
��ME=DN����CME=��CDN��
�ߡ�1=��2��
��180�㩁��CME����1=180�㩁��CDN����2��
���DHM=��DCM=60�㣻
��2��
�⣺DF+EGΪ��ֵ��
���ɣ���MF=FC=x����CG=NG=4��x��
��DF= ![]() x��EG=
x��EG= ![]() ��4��x����
��4��x����
��DF+GE= ![]() x+
x+ ![]() ��4��x��=4
��4��x��=4 ![]() ��
��
��3��![]()
����������3���⣺��ͼ�ۣ�����C�ɵ�M�Ƶ���Nʱ����H�Ƶ���·����Ϊ ![]() ��
��
�ߡ�MHD=60�㣬
���MHN=120�㣬
���MPN=60�㣬
���MON=120�㣬
��MN=8��
��OM=ON= ![]() ��
��
���H�Ƶ���·������= ![]() =
= ![]() ��
��
���Դ��ǣ� ![]() ��
��
�����㾫����������Ŀ����֪���������������ε��ڽǺ���Ǻ͵ȱ������ε����ʵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���������ε������ڽ��У�ֻ������һ���ڽ���ֱ�ǻ�۽ǣ�ֱ�������ε�������ǻ��ࣻ�����ε�һ����ǵ��ں��������ڵ������ڽǵĺͣ������ε�һ����Ǵ����κ�һ�����������ڵ��ڽǣ��ȱ������ε������Ƕ���Ȳ���ÿ���Ƕ���60�㣮