题目内容
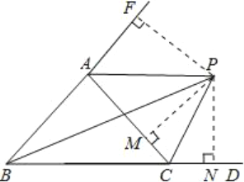
【题目】如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,若∠BPC=40°,则∠CAP=( )

A. 40°B. 45°C. 50°D. 60°
【答案】C
【解析】
根据外角与内角性质得出∠BAC的度数,再利用角平分线的性质以及直角三角形全等的判定,得出∠CAP=∠FAP,即可得出答案.
解:延长BA,作PN⊥BD,PF⊥BA,PM⊥AC,
设∠PCD=x°,
∵CP平分∠ACD,
∴∠ACP=∠PCD=x°,PM=PN,
∵BP平分∠ABC,
∴∠ABP=∠PBC,PF=PN,
∴PF=PM,
∵∠BPC=40°,
∴∠ABP=∠PBC=∠PCD﹣∠BPC=(x﹣40)°,
∴∠BAC=∠ACD﹣∠ABC=2x°﹣(x°﹣40°)﹣(x°﹣40°)=80°,
∴∠CAF=100°,
在Rt△PFA和Rt△PMA中,
![]() ,
,
∴Rt△PFA≌Rt△PMA(HL),
∴∠FAP=∠PAC=50°.
故选:C.

练习册系列答案
相关题目