题目内容
【题目】已知点O是正方形ABCD对角线BD的中点．
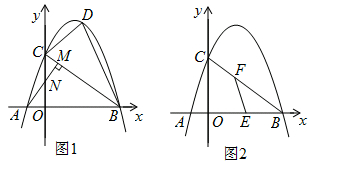
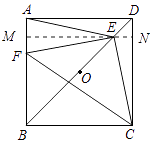
（1）如图1，若点E是OD的中点，点F是AB上一点，且使得∠CEF=90°，过点E作ME∥AD，交AB于点M，交CD于点N．
①∠AEM=∠FEM； ②点F是AB的中点；
（2）如图2，若点E是OD上一点，点F是AB上一点，且使 
= 
= 
，请判断△EFC的形状，并说明理由；
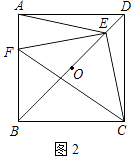
（3）如图3，若E是OD上的动点（不与O，D重合），连接CE，过E点作EF⊥CE，交AB于点F，当 
= 
时，请猜想 的值（请直接写出结论）．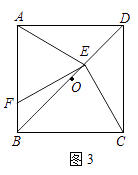
【答案】
（1）证明：①∵四边形ABCD是正方形，
∴∠ABD=45°，∠BAD=∠ABC=∠BCD=∠ADC=90°，AE=CE，
∵ME∥AD，
∴ME⊥AB，∠AME=∠BME=∠BAD=90°，∠ENC=∠ADC=90°，
∴△BME是等腰直角三角形，四边形BCNM是矩形，
∴BM=EM，BM=CN，
∴EM=CN，
在Rt△AME和Rt△ENC中， 
，
∴Rt△AME≌Rt△ENC（HL），
∴∠AEM=∠ECN，
∵∠CEF=90°，
∴∠FEM+∠CEN=90°，
∵∠ECN+∠CEN=90°，
∴∠FEM=∠ECN，
∴∠AEM=∠FEM；
②在△AME和△FME中，∠AME=∠FME=90°，∠AEM=∠FEM，
∴∠EAF=∠EFA，
∴AE=FE，
∵ME⊥AF，
∴AM=FM，
∴AF=2AM，
∵点E是OD的中点，O是BD的中点，
∴ 
= 
，
∵ME∥AD，
∴ 
= ，
∴ 
= 
，
∴点F是AB的中点；
（2）解：△EFC是等腰直角三角形；理由如下：
过点E作ME∥AD，交AB于点M，交CD于点N．如图所示：
同（1）得：AE=CE，Rt△AME≌Rt△ENC，
∴∠AEM=∠ECN，
∵ 
= 
，O是DB的中点，
∴ = 
，
∵ME∥AD，
∴ = ，
∵ = ，
∴AF=2AM，即M是AF的中点，
∵ME⊥AB，
∴AE=FE，
∴∠AEM=∠FEM，FE=CE，
∵∠ECN+∠CEN=90°，
∴∠FEM+∠CEN=90°，
∴∠CEF=90°，
∴△EFC是等腰直角三角形；
（3）解：当 = 
时， = 
；理由同（1）．
【解析】（1）由正方形的对称性可知AE=CE，再结合其他条件可证出Rt△AME≌Rt△ENC，可得∠AEM=∠ECN，再由同角的余角相等证出结论；由平行线分线段成比例定理可得
,DN=AM,AF=2AM,即AF=AB,即点F是AB的中点；（2）模仿第（1）题的图形，缺少过E的MN水平线，因此需要作这条辅助线，同（1）得：AE=CE，Rt△AME≌Rt△ENC，再模仿（1）的方法，运用平行线分线段成比例定理，得出结论；（3）类比（1）
.
,二者存在2倍关系，可猜想
,证法同（1），需作水平的MN线.
【考点精析】认真审题，首先需要了解相似三角形的性质(对应角相等，对应边成比例的两个三角形叫做相似三角形)，还要掌握相似三角形的判定(相似三角形的判定方法:两角对应相等，两三角形相似（ASA）；直角三角形被斜边上的高分成的两个直角三角形和原三角形相似； 两边对应成比例且夹角相等，两三角形相似（SAS）；三边对应成比例，两三角形相似（SSS）)的相关知识才是答题的关键．
