题目内容
【题目】(1)如图1,将两块直角三角尺的直角顶点C叠放在一起,若∠DCE=35°,则∠ACB=_____;若∠ACB=140°,则∠DCE=_______;
(2)猜想∠ACB与∠DCE的大小有何特殊关系,并说明理由;
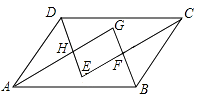
(3)如图2,若是两个同样的直角三角尺60°锐角的顶点A重合在一起,则∠DAB与∠CAE的大小又有何关系,请说明理由.

【答案】(1)∠ACB =145°,∠DCE =40°;(2)∠ACB+∠DCE=180°(或∠ACB与∠DCE互补);(3)∠DAB+∠CAE=120°.
【解析】
(1)本题已知两块直角三角尺实际就是已知三角板的各个角的度数,根据角的和差就可以求出∠ACB,∠DCE的度数;
(2)根据前两个小问题的结论猜想∠ACB与∠DCE的大小关系,结合前两问的解决思路得出证明;
(3)根据(1)(2)解决思路确定∠DAB与∠CAE的大小并证明.
(1) ∵∠ECB=90°,∠DCE=35°
∴∠DCB=90°-35°=55°
∵∠ACD=90°
∴∠ACB=∠ACD+∠DCB=145°,
∵∠ACB=140°,∠ACD=90°
∴∠DCB=140°-90°=50°
∵∠ECB=90°
∴∠DCE=90°-50°=40°,
故答案为:145°,40°
(2)猜想得∠ACB+∠DCE=180°(或∠ACB与∠DCE互补)
理由:
∵∠ECB=90°,∠ACD=90°
∴∠ACB=∠ACD+∠DCB=90°+∠DCB
∠DCE=∠ECB-∠DCB=90°-∠DCB.
∴∠ACB+∠DCE=180°.
(3)∠DAB+∠CAE=120°
理由如下:
∵∠DAE+∠CAE=∠DAC=60,∠CAB+∠CAE=∠BAE=60°
又∵∠DAB=∠DAE+∠CAE+∠CAB
∴∠DAB+∠CAE=∠DAE+∠CAE+∠CAB+∠CAE=∠DAC+∠BAE=120°