题目内容
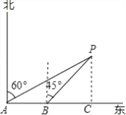
【题目】如图,一艘轮船以18海里/时的速度由西向东方向航行,行至A处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,求轮船与灯塔的最短距离.(精确到0.1, ![]() ≈1.73)
≈1.73)

【答案】轮船与灯塔的最短距离约为8.2海里.
【解析】试题分析:过点P作PC⊥AB于C点,即PC的长为轮船与灯塔的最短距离,根据题意可得AB=6海里,BC=PC,在Rt△PAC中,tan30°=![]() =
=![]() ,由此求得PC的长,即可得轮船与灯塔的最短距离.
,由此求得PC的长,即可得轮船与灯塔的最短距离.
试题解析:
解:过点P作PC⊥AB于C点,即PC的长为轮船与灯塔的最短距离,根据题意,得
AB=18×![]() =6,∠PAB=90°﹣60°=30°,∠PBC=90°﹣45°=45°,∠PCB=90°,
=6,∠PAB=90°﹣60°=30°,∠PBC=90°﹣45°=45°,∠PCB=90°,
∴PC=BC,在Rt△PAC中,tan30°=![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得PC=3![]() +3≈8.2(海里),∴轮船与灯塔的最短距离约为8.2海里.
+3≈8.2(海里),∴轮船与灯塔的最短距离约为8.2海里.

练习册系列答案
相关题目




