题目内容
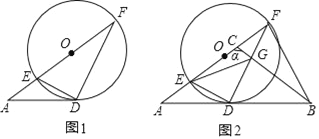
【题目】如图:AD与⊙O相切于点D,AF经过圆心与圆交于点E、F,连接DE、DF,且EF=6,AD=4.
(1)证明:AD2=AEAF;
(2)延长AD到点B,使DB=AD,直径EF上有一动点C,连接CB交DF于点G,连接EG,设∠ACB=α,BG=x,EG=y.
①当α=900时,探索EG与BD的大小关系?并说明理由;
②当α=1200时,求y与x的关系式,并用x的代数式表示y.
【答案】(1)证明见解析;(2)①当α=90°时,EG>BD,理由见解析;②当α=120°时,y=![]() .
.
【解析】试题分析:(1)连接OD,由AD是⊙O的切线,根据切线的性质可得OD⊥AD,即∠ADE+∠EDO=90°,再由EF是直径,根据圆周角定理的推论可得∠EDF=90°,即∠EDO+∠ODF=90°,即可得∠ADE=∠ODF,再由OD=OF,根据等腰三角形的性质可得∠ODF=∠OFD,所以∠ADE=∠OFD,即可判定△ADE∽△AFD,根据相似三角形的性质可得![]() ,即AD2=AEAF;(2)①当α=90°时,EG>BD,理由如下:取EG的中点H,连接CH、DH、CD,在Rt△EDG、Rt△ECG中,点H为EG的中点,根据直角三角形斜边的中线等于斜边的一半可得CH=EH=GH=DH=
,即AD2=AEAF;(2)①当α=90°时,EG>BD,理由如下:取EG的中点H,连接CH、DH、CD,在Rt△EDG、Rt△ECG中,点H为EG的中点,根据直角三角形斜边的中线等于斜边的一半可得CH=EH=GH=DH=![]() EG,根据圆的定义即可判定点C、E、D、G在以点H为圆心,EG为直径的圆上,根据直径是圆中最长的弦可得EG>CD,在Rt△ABC中,DB=AD,再由直角三角形斜边的中线等于斜边的一半可得CD= DB=AD=
EG,根据圆的定义即可判定点C、E、D、G在以点H为圆心,EG为直径的圆上,根据直径是圆中最长的弦可得EG>CD,在Rt△ABC中,DB=AD,再由直角三角形斜边的中线等于斜边的一半可得CD= DB=AD=![]() AB,即可得结论EG>BD;②当α=120°时,将△ADE绕着点D旋转180°,得到△BDP,连接GP,由(1)AD2=AEAF可得16=AE(AE+6),解得AE=2或AE=-8(舍去),因△ADE≌△BDP,根据全等三角形的性质可得ED=DP,AE=BP=2,∠A=∠DBP,再由∠EDF=90°可得DG垂直平分EP,根据线段垂直平分线的性质可得GE=GP=y,因∠A+∠ABC=180°-120°=60°所以∠DBP+∠ABC=60°,即∠GBP=60°;过点P作PQ⊥BG,在Rt△BPQ中,∠GBP=60°,BP=2,可求得BQ=1,PQ=
AB,即可得结论EG>BD;②当α=120°时,将△ADE绕着点D旋转180°,得到△BDP,连接GP,由(1)AD2=AEAF可得16=AE(AE+6),解得AE=2或AE=-8(舍去),因△ADE≌△BDP,根据全等三角形的性质可得ED=DP,AE=BP=2,∠A=∠DBP,再由∠EDF=90°可得DG垂直平分EP,根据线段垂直平分线的性质可得GE=GP=y,因∠A+∠ABC=180°-120°=60°所以∠DBP+∠ABC=60°,即∠GBP=60°;过点P作PQ⊥BG,在Rt△BPQ中,∠GBP=60°,BP=2,可求得BQ=1,PQ=![]() ,所以GQ=BG-BQ=x-1,在Rt△GPQ中, PQ=
,所以GQ=BG-BQ=x-1,在Rt△GPQ中, PQ=![]() ,GQ=x-1,GP=y,由勾股定理可得PG2=GQ2+PQ2,即y2=(x-1) 2+(
,GQ=x-1,GP=y,由勾股定理可得PG2=GQ2+PQ2,即y2=(x-1) 2+(![]() ) 2 ,整理即可得y=
) 2 ,整理即可得y=![]() .
.
试题解析:
(1)证明:连接OD
∵AD是⊙O的切线
∴OD⊥AD,即∠ADE+∠EDO=90°
∵EF是直径

∴∠EDF=90°,即∠EDO+∠ODF=90°
∴∠ADE=∠ODF
∵OD=OF
∴∠ODF=∠OFD
∴∠ADE=∠OFD
∴△ADE∽△AFD
∴![]() ,即
,即![]()
(2)①当![]() 时,EG>BD
时,EG>BD
理由如下:取EG的中点H,连接CH、DH、CD,
∵Rt△EDG、Rt△ECG,点H为EG的中点
∴CH=EH=GH=DH= ![]()
∴点C、E、D、G在以点H为圆心,EG为直径的圆上

∴EG>CD
∵Rt△ABC, DB=AD
∴CD= DB=AD= ![]()
∴EG>BD
②当![]() 时
时
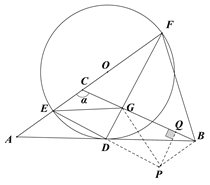
将△ADE绕着点D旋转180°,得到△BDP,连接GP
由(1)![]() 得:
得: ![]() ,解得AE=2或AE=-8(舍去)
,解得AE=2或AE=-8(舍去)
∴△ADE≌△BDP
∴ED=DP,AE=BP=2,∠A=∠DBP
∵∠EDF=90°
∴DG垂直平分EP
∴GE=GP= ![]()
∵∠A+∠ABC=180°-120°=60°
∴∠DBP+∠ABC=60°,即∠GBP=60°
过点P作PQ⊥BG
在Rt△BPQ中,∠GBP=60°,BP=2
∴BQ=1,PQ=![]()
∴GQ=BG-BQ= ![]() -1
-1
在Rt△GPQ中, PQ=![]() ,GQ=
,GQ= ![]() -1,GP=
-1,GP= ![]()
∴![]()
即![]()
![]()

 名校通行证有效作业系列答案
名校通行证有效作业系列答案