��Ŀ����
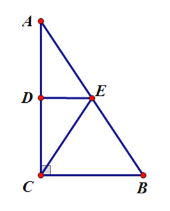
����Ŀ����ͼ���ڱ߳�Ϊ![]() ����λ���ȵ�С��������ɵ������У������˸��
����λ���ȵ�С��������ɵ������У������˸��![]() ��
��![]() �������������ߵĽ��㣩����
�������������ߵĽ��㣩����![]() ��
��![]() ����Ϊ
����Ϊ![]() ��
��![]() ��
��
![]() �۲�ͼ����գ�
�۲�ͼ����գ�![]() ����
����![]() ��________��˳ʱ����ת________�ȵõ��ģ�
��________��˳ʱ����ת________�ȵõ��ģ�
![]() ��
��![]() �е�ͼ����Ϊһ���µ�������ͼ���������µĻ���ͼ����
�е�ͼ����Ϊһ���µ�������ͼ���������µĻ���ͼ����![]() ��˳ʱ����ת
��˳ʱ����ת![]() �ȣ���������ת���ͼ�Σ����У�
�ȣ���������ת���ͼ�Σ����У�![]() ��
��![]() ��
��![]() ��
��![]() �Ķ�Ӧ��ֱ�Ϊ
�Ķ�Ӧ��ֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ����������
����������![]() ��
��![]() ��
��![]() ��
��![]() �����ı���
�����ı���![]() ����״Ϊ________��
����״Ϊ________��
![]() ��
��![]() ��Ϊλ�����ģ�λ�Ʊ�Ϊ
��Ϊλ�����ģ�λ�Ʊ�Ϊ![]() ��ԭͼ����ͼ��Ӧ�ߵı�Ϊ
��ԭͼ����ͼ��Ӧ�ߵı�Ϊ![]() ���������ı���
���������ı���![]() ��λ��ͼ�Σ�
��λ��ͼ�Σ�

���𰸡�O,90,������
��������
��1������OB=OB1��OA=OA1����AOA1=��BOB1=90�㣬�������ת�Ķ��壬�ѡ�OAB��O��˳ʱ����ת90�ȿɵõ���OA1B1��
��2�����ݹ���ԭ��ԳƵĵ����������д��A��B��A1��B1�Ķ�Ӧ��ֱ�ΪA2��B2��A3��B3�����꣬Ȼ����㼴�ɵõ��ı���BB1B2B3��Ȼ�������ת�����ʵõ��Խ����ഹֱƽ������ȿ��ж��ı���BB1B2B3Ϊ
������
��3���ѵ�B��B1��B2��B3�ĺ������궼����2�õ���Ӧ��C��D��E��F�����꣬Ȼ����㼴�ɵõ��ı���CDEF��
�⣺��1����OA1B1���ɡ�OAB��O��˳ʱ����ת90�ȵõ��ģ�
��2����ͼ1���ı���BB1B2B3��Ϊ���������������Σ�
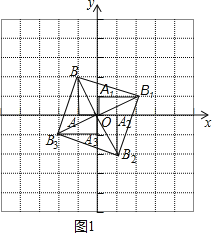
��3����ͼ2���ı���CDEFΪ������
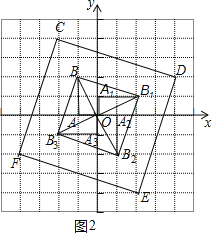
�ʴ�ΪO��90�������Σ�