题目内容
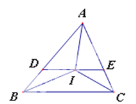
【题目】如图,△ABC中,IB,IC分别平分∠ABC,∠ACB,过I点作DE∥BC,分别交AB于D,交AC于E,给出下列结论:①△DBI是等腰三角形;②△ACI是等腰三角形;③AI平分∠BAC;④△ADE周长等于AB+AC,其中正确的是: ___________(只需填写序号)。
【答案】①③④.
【解析】
根据角平分线的性质、平行线的性质、等腰三角形的判定与性质分别对各选项分析判断后利用排除法求解.
解:∵IB平分∠ABC,
∴∠DBI=∠CBI,
∵DE∥BC,
∴∠DIB=∠CBI,
∴∠DBI=∠DIB,
∴BD=DI,
∴△DBI是等腰三角形,故①正确;
∵∠BAC不一定等于∠ACB,
∴∠IAC不一定等于∠ICA,
∴△ACI不一定是等腰三角形,故②错误;
∵三角形角平分线相交于一点,BI,CI分别是∠ABC和∠ACB的平分线,
∴AI平分∠BAC,故③正确;
∵BD=DI,同理可得EI=EC,
∴△ADE的周长=AD+DI+EI+AE=AD+BD+EC+AE=AB+AC,故④正确;
其中正确的是①③④,
故填:①③④.

练习册系列答案
相关题目