题目内容
【题目】如果α，β（α≠β）是一元二次方程x2+2x﹣1=0的两个根，则α2+α﹣β的值是_____．
【答案】3
【解析】分析：把α代入一元二次方程x2+2x﹣1=0，可得α2+2α﹣1=0，再利用两根之和α+β=﹣2，将式子变形后，整理代入，即可求值.
详解：∵α，β（α≠β）是一元二次方程x2+2x﹣1=0的两个根，
∴α2+2α﹣1=0，α+β=﹣2，
∴α2+α=1﹣α，
∴α2+α﹣β=1﹣α﹣β=1+2=3，
故答案为3
点睛:本题考查了一元二次方程根与系数的关系，及一元二次方程的解，一元二次方程ax+bx+c=0,(a≠0),当b-4ac≥0时，方程有解，
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】如图1，将边长为1的正方形ABCD压扁为边长为1的菱形ABCD．在菱形ABCD中，∠A的大小为α，面积记为S．
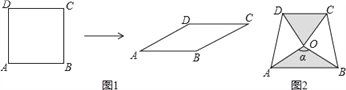
（1）请补全表：
α | 30° | 45° | 60° | 90° | 120° | 135° | 150° |
S |
| 1 |
|
（2）填空：由（1）可以发现单位正方形在压扁的过程中，菱形的面积随着∠A大小的变化而变化，不妨把单位菱形的面积S记为S（α）．例如：当α=30°时，S=S（30°）=
；当α=135°时，S=S=
．由上表可以得到S（60°）=S（ °）；S（30°）=S（ °），…，由此可以归纳出S（α）=（ °）．
（3）两块相同的等腰直角三角板按图2的方式放置，AD=
，∠AOB=α，试探究图中两个带阴影的三角形面积是否相等，并说明理由（注：可以利用（2）中的结论）．
【题目】某商场投入13 800元资金购进甲、乙两种矿泉水共500箱，矿泉水的成本价和销售价如表所示：
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该商场购进甲、乙两种矿泉水各多少箱？
(2)全部售完500箱矿泉水，该商场共获得利润多少元？