题目内容
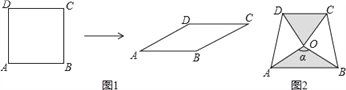
【题目】如图1，将边长为1的正方形ABCD压扁为边长为1的菱形ABCD．在菱形ABCD中，∠A的大小为α，面积记为S．
（1）请补全表：
α | 30° | 45° | 60° | 90° | 120° | 135° | 150° |
S |
| 1 |
|
（2）填空：由（1）可以发现单位正方形在压扁的过程中，菱形的面积随着∠A大小的变化而变化，不妨把单位菱形的面积S记为S（α）．例如：当α=30°时，S=S（30°）=
；当α=135°时，S=S=
．由上表可以得到S（60°）=S（ °）；S（30°）=S（ °），…，由此可以归纳出S（α）=（ °）．
（3）两块相同的等腰直角三角板按图2的方式放置，AD=
，∠AOB=α，试探究图中两个带阴影的三角形面积是否相等，并说明理由（注：可以利用（2）中的结论）．
【答案】(1) 表中依次填写： 
； 
； 
； 
;(2) 120；30；α；(3) 两个带阴影的三角形面积相等,理由见解析.
【解析】试题分析：（1）根据α，求出AB边上的高，从而用底×高得到菱形的面积；（2）在表格中找出面积相等时，角度的对应关系；（3）利用（2）中的结论求解。
试题解析：（1）当α=45°时过D作DE⊥AB于点E，
则DE=
AD=
，∴S=ABDE=
，同理当α=60°时S=
，
当α=120°时，如图2，过D作DF⊥AB，交BA的延长线于点F，
则∠DAE=60°，∴DF=AD=，∴S=ABDF=
，
同理当α=150°时，可求得S=
，故表中依次填写：
；；
；
；
（2）由（1）可知S（60°）=S，S=S（30°），∴S=S（α）故答案为：120；30；α；
（3）两个带阴影的三角形面积相等．
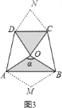
证明：如图3将△ABO沿AB翻折得到菱形AMBO，将△CDO沿CD翻折得到菱形OCND．∵∠AOD=∠COB=90°，∴∠COD+∠AOB=180°，∴S△AOB=S菱形AMBO=S（α）S△CDO=
S
S由（2）中结论S（α）=S∴S△AOB=S△CDO．
