题目内容
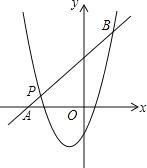
【题目】有理数a，b，c在数轴上的位置如图所示，且|a|=|b|．
（1）用“＞”“＜”或“=”填空：
b______0，a+b______0，a-c______0，b-c______0；
（2）化简：|c-a|-|c-b|+|a+b|．
【答案】（1）＜， = ，＞，＜；（2）a+b-2c．
【解析】
（1）根据数轴上右边的点表示的数比左边的点表示的数大可以解答本题；
（2）根据数轴可以将题目中式子的绝对值去掉，然后化简即可解答本题．
解：（1）由数轴可得，
b＜c＜0＜a，
∵|a|=|b|，
∴b＜0，a+b=0，a-c＞0，b-c＜0，
故答案为：＜，=，＞，＜；
（2）由数轴可得，
b＜c＜0＜a，
∵|a|=|b|，
∴|c-a|-|c-b|+|a+b|
=a-c-（c-b）+0
=a-c-c+b
=a+b-2c．
练习册系列答案
全优测试卷系列答案
冲刺100分1号卷系列答案
相关题目
