Question

【题目】如图，点P是菱形ABCD对角线AC上的一点，连接DP并延长DP交边AB于点E，连接BP并延长交边AD于点F，交CD的延长线于点G．已知DF：FA＝1：2．

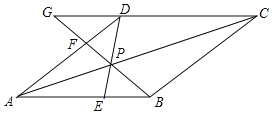
（1）求证：△APB≌△APD；

（2）当线段DP的长为6时，求线段FG的长；

（3）请直接写出的比值．

Answer 1

【答案】（1）详见解析；（2）线段FG的长为5；（3）．

【解析】

（1）由菱形的性质知∠BAP＝∠DAP，AB＝AD，再结合AP＝AP即可证得△APB≌△APD；

（2）首先证明△AFP∽△CBP，得出，由知，根据PB＝PD知PF＝PD，结合DP＝6可得FB＝10，再证△DFG∽△AFB得，从而得出答案；

（3）由△APF∽△CBP，且知＝（）2＝，由S△ABC＝S△ADC，S△ABP＝S△ADP知S△PBC＝S△PDC，即可得出答案．

解：（1）由菱形的性质知∠BAP＝∠DAP，AB＝AD，

在△APB和△APD中，

∵，

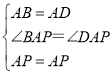∴△APB≌△APD（SAS）；

（2）∵四边形ABCD是菱形，

∴AD∥BC，AD＝BC，

∴△AFP∽△CBP，

∴．

∵，

∴，

∴

由（1）知PB＝PD，

∴．

∴PF＝PD，

当DP＝6时，PF＝×6＝4，

∴FB＝FP+PB＝4+6＝10．

∵DG∥AB，

∴△DFG∽△AFB．

∴，

∴FG＝×10＝5

（3）由（2）知△APF∽△CBP，且

∴＝（）2＝，

又∵S△ABC＝S△ADC，S△ABP＝S△ADP，

∴S△PBC＝S△PDC，

∴=