题目内容
【题目】在边长为2的正方形ABCD中，点P、Q分别是边AB、BC上的两个动点（与点A、B、C不重合），且始终保持BP=BQ，AQ⊥QE，QE交正方形外角平分线CE于点E，AE交CD于点F，连结PQ.
（1）求证：△APQ≌△QCE；
（2）求∠QAE的度数；
（3）设BQ=x，当x为何值时，QF∥CE，并求出此时△AQF的面积.
【答案】（1）证明见解析；（2）45°；（3）当x=-2+2
时，S=-4+4.
【解析】
试题（1）判断出△PBQ是等腰三角形，然后求出∠APQ=∠QCE=135°，再根据同角的余角相等求出∠PAQ=∠CQE，再求出AP=CQ，然后利用“角边角”证明即可；
（2）根据全等三角形对应边相等可得AQ=EQ，判断出△AQE是等腰三角形，再根据等腰三角形的性质解答；
（3）把△ABQ绕点A逆时针旋转90°得到△ADG，求出∠GAF=45°，从而得到∠GAF=∠QAF，再利用“边角边”证明△AQF和△AGF全等，根据全等三角形的对应边相等可得QF=GF，再根据两直线平行，同位角相等求出∠CQF=45°，然后求出CQ=CF，分别用x求出CQ、CF，利用勾股定理列式求出QF，然后列出方程求出x，再求出△AGF的面积，即为△AQF的面积.
试题解析：（1）∵ 四边形ABCD是正方形，
∴ AB=BC，∠B=∠BCD=∠DCM=90°，
∵ BP=BQ，
∴ △PBQ是等腰直角三角形，AP=QC，
∴ ∠BPQ=45°，
∴ ∠APQ=135°
∵ CE平分∠DCM，
∴ ∠DCE=∠ECM=45°，
∴ ∠QCE=135°，
∴ ∠APQ=∠QCE=135°，
∵ AQ⊥QE，即 ∠AQE=90°,
∴ ∠AQB+∠CQE=90°．
∵ ∠AQB+∠BAQ=90°．
∴ ∠BAQ=∠CQE．
∴ △APQ≌△QCE（ASA）．
（2）由（1）知△APQ≌△QCE．∴ QA=QE.
∵ ∠AQE=90°，
∴ △AQE是等腰直角三角形，∴ ∠QAE=45°
（3）连结AC，若QF∥CE，则∠FQC=∠ECM=45°.
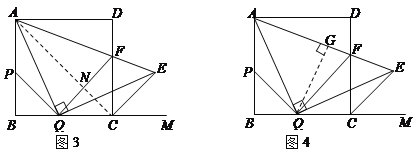
∴ △QCF是等腰直角三角形，∴ CF=CQ=2-x, ∴ DF=BQ=x.
∵ AB=AD，∠B=∠D=90°，
∴ △ABQ≌△ADF（SAS）.
∴ AQ=AF，∠QAB=∠DAF=22.5°,
∴ AC垂直平分QF，
∴ ∠QAC=∠FAC=∠QAB=∠FAD=22.5°, FQ=2QN，
∴ FQ=2BQ=2x.
在Rt△QCF中，根据勾股定理，得(2-x)2+(2-x)2=(2x)2.
解这个方程，得 x1=-2+2, x2=-2-2(舍去).
∴ 当x=-2+2时，QF∥CE.
此时，S△QCF=S△QEF，
∴ S△QCF+ S△AQF=S△QEF+ S△AQF= S△AQE=
AQ2，
∴ S△AQF= S△AQE- S△QCF=AQ2-CQ2=(AQ2-CQ2)
=[(x2+22)-(2-x)2]=·4x=2x=-4+4.
