题目内容
【题目】完成下面的证明过程:
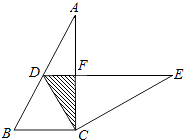
已知:如图,∠D=110°,∠EFD=70°,∠1=∠2,
求证:∠3=∠B

证明:∵∠D=110°, ∠EFD=70°(已知)
∴∠D+∠EFD=180°
∴AD∥______( )
又∵∠1=∠2(已知)
∴_____∥BC ( 内错角相等,两直线平行)
∴EF∥_____ ( )
∴∠3=∠B(两直线平行,同位角相等)
【答案】详见解析.
【解析】
求出∠D+∠EFD=180°,根据平行线的判定推出AD∥EF,AD∥BC,即可推出答案.
证明:∵∠D=110°, ∠EFD=70°(已知)
∴∠D+∠EFD=180°
∴AD∥_EF_( 同旁内角互补,两直线平行 )
又∵∠1=∠2(已知)
∴AD∥BC ( 内错角相等,两直线平行)
∴EF∥_BC_ ( 平行于同一直线的两直线平行 )
∴∠3=∠B(两直线平行,同位角相等) .

练习册系列答案
相关题目
【题目】在下图的直角坐标系中,将△ABC平移后得到△A’B’C’,它们的个顶点坐标如下表所示
△ABC | A(0,0) | B(3,0) | C(5,5) |
△A'B'C' | A'(4,2) | B'(7,b) | C'(c,d) |
(1)观察表中各对应点坐标的变化,并填空:△ABC向______平移______个单位长度,再向______平移______个单位长度可以得到△A'B'C';
(2)在坐标系中画出△ABC及平移后的△A'B'C';
(3)求出△A'B'C'的面积.