题目内容
【题目】如图,在ABCD中,AC、BD交于点O,BD⊥AD于点D,将△ABD沿BD翻折得到△EBD,连接EC、EB.
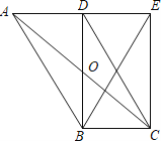
(1)求证:四边形DBCE是矩形;
(2)若BD=4,AD=3,求点O到AB的距离.
【答案】(1)见解析;(2)点O到AB的距离为![]() .
.
【解析】
(1)先利用折叠的性质和平行四边形的性质得出DE∥BC,DE=BC,则四边形DBCE是平行四边形,再利用BE=CD即可证明四边形DBCE是矩形;
(2)过点O作OF⊥AB,垂足为F,先利用勾股定理求出AB的长度,然后利用![]() 面积即可求出OF的长度,则答案可求.
面积即可求出OF的长度,则答案可求.
(1)由折叠性质可得:AD=DE,BA=BE,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,BA=CD,
∴DE∥BC,DE=BC,
∴四边形DBCE是平行四边形,
又∵BE=CD,
∴四边形DBCE是矩形.
(2)过点O作OF⊥AB,垂足为F,

∵BD⊥AD,
∴∠ADB=90°,
在Rt△ADB中,BD=4,AD=3,
由勾股定理得:AB=![]() ,
,
又∵四边形ABCD是平行四边形,
∴OB=OD=![]() ,
,
![]()
∴![]()
答:点O到AB的距离为![]() .
.

练习册系列答案
相关题目