题目内容
【题目】如图,直线y=ax+b交x轴于点A,交y轴于点B,且a,b满足a=![]() +4,直线y=kx﹣4k过定点C,点D为直线y=kx﹣4k上一点,∠DAB=45°.
+4,直线y=kx﹣4k过定点C,点D为直线y=kx﹣4k上一点,∠DAB=45°.
(1)a= ,b= ,C坐标为 ;
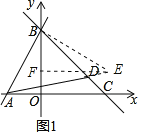
(2)如图1,k=﹣1时,求点D的坐标;
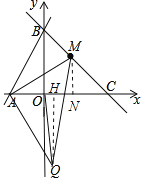
(3)如图2,在(2)的条件下,点M是直线y=kx﹣4k上一点,连接AM,将AM绕A顺时针旋转90°得AQ,OQ最小值为 .
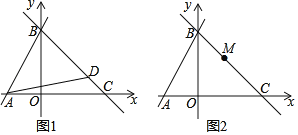
【答案】(1)4;4;(4,0);(2)D(![]() ,
,![]() );(3)2
);(3)2![]() .
.
【解析】
(1)根据二次根式有意义的条件分别求出a、b,根据一次函数图象上点的坐标特征求出点C的坐标
(2)分D在线段BC上、D在线段CB的延长线上两种情况,证明△AOB≌△BFE,根据全等三角形的性质、一次函数的性质计算;
(3)证明△ANM≌△QHA,得到MN=AH=-m+4,AN=QH=m+1,根据勾股定理、二次根式的性质解答即可.
解:(1)∵4-b≥0,b-4≥0,
∴b=4,
则a=4,
对于直线y=kx-4k,当y=0时,x=4,
∴点C的坐标为(4,0),
故答案为:4;4;(4,0);
(2)当D在线段BC上时,作BE⊥BA交AD的延长线于点E,作EF⊥y轴于F,
则∠BEF+∠EBO=90°,∠ABO+∠EBO=90°,
∴∠BEF=∠ABO,
∵∠DAB=45°,
∴BA=BE,
在△AOB和△BFE中,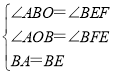 ,
,
∴△AOB≌△BFE(AAS),
∴BF=OA,EF=OB=4,
对于直线y=4x+4,当y=0时,x=-1,
∴OA=1,
∴E(4,3)
设直线AE解析式为y=mx+n,![]() ,
,
解得,![]() ,
,
则直线AE解析式为y=![]() x+
x+![]() ,
,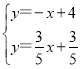 ,
,
解得,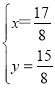 ,
,
∴D(![]() ,
,![]() );
);
当D在CB延长线上时,同理可得D(![]() );
);
(3)设M(m,-m+4),
由(2)可得,△ANM≌△QHA,
∴MN=AH=-m+4,AN=QH=m+1,
∴Q(-m+3,-m-1)
当m=1时,OQ最小为2![]() ,
,
故答案为:2![]() .
.

 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案