��Ŀ����
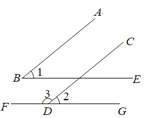
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�A��m��0����B��n��0����C����1��2����������ʽ|m+2|+��m+n��2��2��0��
��1�����m��n��ֵ��
��2������x����������ϴ���һ��M��ʹ��COM�����������ABC�������һ�룬�����M�����ꣻ
���������������λ���Ƿ���ڵ�M��ʹ��COM�����������ABC�������һ����Ȼ�����������ڣ���ֱ���������ĺ�����д�����������ĵ�M�����ꣻ
��3����ͼ2������C��CD��y�ύy���ڵ�D����PΪ�߶�CD�ӳ�����һ���㣬����OP��OEƽ�֡�AOP��OF��OE������P�˶�ʱ��![]() ��ֵ�Ƿ��ı䣿�����䣬����ֵ�����ı䣬˵�����ɣ�
��ֵ�Ƿ��ı䣿�����䣬����ֵ�����ı䣬˵�����ɣ�

���𰸡���1��m=��2��n=4����2����M������Ϊ��3��0�����ڵ�M������Ϊ��3��0����3��0����0��6����0����6������3��2��
��������
��1�����ݷǸ����������г������飬�ⷽ���鼴�ɣ�
��2���ٸ��������ε������ʽ���㼴�ɣ�
�ڷֵ�M��x��y��������������㣻
��3�����ݽ�ƽ���ߵĶ��塢��ֱ�Ķ���õ���POF=��BOF�����POF=��BOF=x����DOE=y�����ͼ�εõ�x=y���õ��𰸣�
��1��������ã�![]() ����ã�
����ã�![]() ����m=��2��n=4��
����m=��2��n=4��
��2�������M�����������Ϊ��x��0������ABC�����![]() 6��2=6��������ã�
6��2=6��������ã�![]() x��2
x��2![]() 6����ã�x=3����COM��������ڡ�ABC�������һ��ʱ����M������Ϊ��3��0����
6����ã�x=3����COM��������ڡ�ABC�������һ��ʱ����M������Ϊ��3��0����
�ڵ���M��x����ʱ���ɢٵã���M������Ϊ��3��0����3��0��������M��y����ʱ�����M�����������Ϊ��0��y����������ã�![]() |y|��1
|y|��1![]() 6����ã�y=��6��
6����ã�y=��6��
�������������������ĵ�M������Ϊ��3��0����3��0����0��6����0����6����
��3��![]() 2������ı䣮
2������ı䣮
��OEƽ�֡�AOP�����EOP=��AOE��
��OF��OE�����EOP+��POF=90�㣬��AOE+��BOF=90�㣬���POF=��BOF�����POF=��BOF=x����DOE=y��
��CD��y�ᣬ��CD��x�ᣬ���OPD=��POB=2x�����POD=90�㩁2x��
�ߡ�EOF=90�㣬��y+90�㩁2x+x=90�㣬��ã�x=y�����OPD=2��DOE����![]() 2��
2��