Question

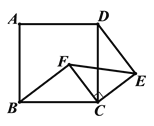
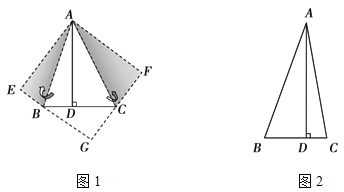
【题目】如图1，在△ABC中，已知∠BAC＝45°，AD⊥BC于D，BD＝2，DC＝3，求AD的长. 小萍同学灵活运用轴对称知识，将图形进行翻折变换如图1.她分别以AB、AC为对称轴，画出△ABD、△ACD的轴对称图形，D点的对称点为E、F，延长EB、FC相交于G点，得到四边形AEGF是正方形.设AD=x，利用勾股定理，建立关于x的方程模型，即可求出x的值.参考小萍的思路，探究并解答新问题：如图2，在△ABC中，∠BAC＝30°，AD⊥BC于D，AD＝4.请你按照小萍的方法画图,得到四边形AEGF，求△BGC的周长.（画图所用字母与图1中的字母对应）

Answer 1

【答案】.

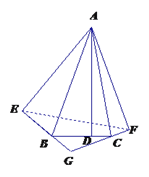
【解析】试题分析：参考做法得到四边形AEGF，连接EF得出△AEF为等边三角形，从而得出EF=4，∠FEG=∠EFG=30°，根据△EFG的性质求出EG的长度，最后根据BG+CG+BC=BG+CG+EB+FC=2EG得出三角形的周长．

试题解析：解： 参考小萍的做法得到四边形AEGF，∠EAF=60°，

∠EGF=120°，∠AEG=∠AFG= 90°，AE=AF=AD=4， 连结EF，可得 △AEF为等边三角形，

∴ EF=4， ∴ ∠FEG=∠EFG= 30°，∴ EG=FG，在△EFG中，可求，

∴△EFG的周长＝BG+CG+BC=BG+CG+EB+FC=2EG=．