题目内容
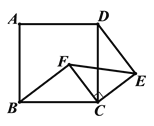
【题目】如图,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF, BC=5,CF=3,BF=4.
求证:DE∥FC
【答案】证明见解析.
【解析】试题分析:根据正方形以及△ECF的性质得出△BCF和△DCE全等,从而得出∠DEC=∠BFC,根据BC、CF和BF的长度得出∠BFC=90°,即∠DEC=90°,最后根据同旁内角互补两直线平行得出答案.
试题解析:∵四边形 ABCD是正方形 ∴∠BCF+∠FCD=90°,BC=CD,
∵△ECF是等腰直角三角形, ∴∠ECD+∠FCD=90°, CF=CE,
∴∠BCF=∠ECD, ∴△BCF≌△DCE,
在△BFC中,BC=5,CF=3,BF=4, ∴ CF2+BF2=BC2 ∴∠BFC=90°,
∵△BCF≌△DCE,∴DE=BF=4,∠BFC=∠DEC=∠FCE=90°,∴DE∥FC.

练习册系列答案
相关题目