题目内容
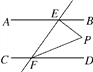
【题目】如图，AB∥CD，EF与AB，CD分别相交于点E，F，EP⊥EF，与∠EFD的平分线FP相交于点P.若∠BEP＝46°，则∠EPF＝________°.
【答案】68
【解析】由AB∥CD，根据两直线平行，同旁内角互补，即可得∠BEF+∠DFE=180°，又由EP⊥EF，∠EFD的平分线与EP相交于点P，∠BEP=46°，即可求得∠PFE的度数，然后根据三角形的内角和定理，即可求得∠EPF的度数．
解：∵AB∥CD，
∴∠BEF+∠DFE=180°，
∴EP⊥EF，
∴∠PEF=90°，
∵∠BEP=36°，
∴∠EFD=180°90°46°=44°，
∵∠EFD的平分线与EP相交于点P，
∴∠EFP =
∠EFD=22°，
∴∠EPF=90°∠EFP=68°.
故答案为：68.
练习册系列答案
阅读快车系列答案
相关题目
