题目内容
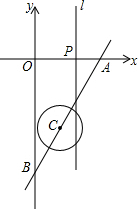 如图,平面直角坐标系的单位是厘米,直线AB的解析式为y=
如图,平面直角坐标系的单位是厘米,直线AB的解析式为y=| 3 |
| 3 |
(1)求A、B两点的坐标;
(2)设⊙C运动的时间为t,当⊙C和坐标轴相切时,求时间t的值.
(3)在点C运动的同时,另有动点P以2cm/秒的速度在线段OA上来回运动,过点P作直线l垂直于x轴.若点C与点P同时分别从点B、点O开始运动,求直线l与⊙C所有相切时点P的坐标.
分析:(1)由直线AB的解析式为y=
x-6
,分别与x 轴y轴相交于A、B 两点,即可求得A、B两点的坐标;
(2)分别从当⊙C与y轴相切时,当⊙C与x轴相切,且在x轴下方时与当⊙C与x轴相切,且在x轴上方时去分析,利用切线的性质由相似三角形的性质,即可求得答案;
(3)分别从第一、二、三、四次相切时去分析求解,又由t≤
,即t≤
,即可求得答案.
| 3 |
| 3 |
(2)分别从当⊙C与y轴相切时,当⊙C与x轴相切,且在x轴下方时与当⊙C与x轴相切,且在x轴上方时去分析,利用切线的性质由相似三角形的性质,即可求得答案;
(3)分别从第一、二、三、四次相切时去分析求解,又由t≤
| 6+1 |
| 1.5 |
| 14 |
| 3 |
解答:解:(1)∵直线AB的解析式为y=
x-6
,分别与x 轴y轴相交于A、B 两点.
∴当x=0时,y=-6
,当y=0时,x=6,
∴A(6,0),B(0,-6
);(2分)
(2)∵A(6,0),B(0,-6
);
∴OA=6,OB=6
,
∴AB=
=12,
当⊙C与y轴相切时,设切点为D,连接CD,
则CD⊥y轴,
∴CD∥OA,
∴△BCD∽△BAO,
∴CD:OA=BC:AB,
即1:6=BC:12,
∴BC=2,
∵动点C从点B出发沿射线BA以3cm/秒的速度运动,
∴t=
;(4分)
当⊙C与x轴相切,且在x轴下方时,
设切点为E,连接CE,则CE⊥x轴,
∴CE∥OB,
∴△AEC∽△AOB,
∴EC:OB=AC:AB,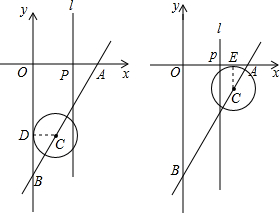
即1:6
=AC:12,
解得:AC=
,
∴BC=AC-EC=12-
,
∴t=4-
;
当⊙C与x轴相切,且在x轴上方时,BC=12+
,
∴t=4+
;(8分)
综上t=
或t=4-
或t=4+
;
(3)∵在Rt△AOB中,tan∠OBA=
=
,
∴∠OBA=30°,
∵动点C从点B出发沿射线BA以3cm/秒的速度运动,
∴⊙C沿x轴正方向的速度为每秒1.5cm,
①第一次相切时,2t-1.5t=1,得:t=2,P1(4,0);(9分)
②第二次相切 2t+1.5t+1=12,得t=
,P2(
,0);(10分)
③第三次相切 2t+1.5t-1=12,得t=
,P3(
,0);(11分)
④第四次相切 2t-12+1=1.5t,得t=22,
∵t≤
,即t≤
,
∴t=22>
(不符合题意舍去);(12分)
综上:p1(4,0)或P2(
,0)或P3(
,0).
| 3 |
| 3 |
∴当x=0时,y=-6
| 3 |
∴A(6,0),B(0,-6
| 3 |
(2)∵A(6,0),B(0,-6
| 3 |
∴OA=6,OB=6
| 3 |
∴AB=
| OA2+OB2 |
当⊙C与y轴相切时,设切点为D,连接CD,
则CD⊥y轴,
∴CD∥OA,
∴△BCD∽△BAO,
∴CD:OA=BC:AB,
即1:6=BC:12,
∴BC=2,
∵动点C从点B出发沿射线BA以3cm/秒的速度运动,
∴t=
| 2 |
| 3 |
当⊙C与x轴相切,且在x轴下方时,
设切点为E,连接CE,则CE⊥x轴,
∴CE∥OB,
∴△AEC∽△AOB,
∴EC:OB=AC:AB,

即1:6
| 3 |
解得:AC=
| 2 |
| 3 |
| 3 |
∴BC=AC-EC=12-
| 2 |
| 3 |
| 3 |
∴t=4-
| 2 |
| 9 |
| 3 |
当⊙C与x轴相切,且在x轴上方时,BC=12+
| 2 |
| 3 |
| 3 |
∴t=4+
| 2 |
| 9 |
| 3 |
综上t=
| 2 |
| 3 |
| 2 |
| 9 |
| 3 |
| 2 |
| 9 |
| 3 |
(3)∵在Rt△AOB中,tan∠OBA=
| OA |
| OB |
| ||
| 3 |
∴∠OBA=30°,
∵动点C从点B出发沿射线BA以3cm/秒的速度运动,
∴⊙C沿x轴正方向的速度为每秒1.5cm,
①第一次相切时,2t-1.5t=1,得:t=2,P1(4,0);(9分)
②第二次相切 2t+1.5t+1=12,得t=
| 22 |
| 7 |
| 40 |
| 7 |
③第三次相切 2t+1.5t-1=12,得t=
| 26 |
| 7 |
| 32 |
| 7 |
④第四次相切 2t-12+1=1.5t,得t=22,
∵t≤
| 6+1 |
| 1.5 |
| 14 |
| 3 |
∴t=22>
| 14 |
| 3 |
综上:p1(4,0)或P2(
| 40 |
| 7 |
| 32 |
| 7 |
点评:此题考查了切线的性质、相似三角形的判定与性质、直线与圆的位置关系以及一次函数的性质.此题综合性较强,难度较大,注意掌握辅助线的作法,注意掌握方程思想、分类讨论思想与数形结合思想的应用.

练习册系列答案
相关题目
 如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线
如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线 =2
=2 如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
 如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.
如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.