题目内容
【题目】抛物线![]() 经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
(1)求此抛物线的解析式;
(2)已知点D![]() 在第四象限的抛物线上,求点D关于直线BC对称的点D’的坐标;
在第四象限的抛物线上,求点D关于直线BC对称的点D’的坐标;
(3)在(2)的条件下,连结BD,问在x轴上是否存在点P,使![]() ,若存在,请求出P点的坐标;若不存在,请说明理由.
,若存在,请求出P点的坐标;若不存在,请说明理由.

【答案】(1)![]()
(2)(0,-1)
(3)(1,0)(9,0)
【解析】
(1)将A(1,0)、C(0,3)两点坐标代入抛物线y=ax2+bx3a中,列方程组求a、b的值即可;
(2)将点D(m,m1)代入(1)中的抛物线解析式,求m的值,再根据对称性求点D关于直线BC对称的点D'的坐标;
(3)分两种情形①过点C作CP∥BD,交x轴于P,则∠PCB=∠CBD,②连接BD′,过点C作CP′∥BD′,交x轴于P′,分别求出直线CP和直线CP′的解析式即可解决问题.
解:(1)将A(1,0)、C(0,3)代入抛物线y=ax2+bx3a中,
得![]() ,
,
解得![]()
∴y=x22x3;
(2)将点D(m,m1)代入y=x22x3中,得
m22m3=m1,
解得m=2或1,
∵点D(m,m1)在第四象限,
∴D(2,3),
∵直线BC解析式为y=x3,
∴∠BCD=∠BCO=45°,CD′=CD=2,OD′=32=1,
∴点D关于直线BC对称的点D'(0,1);
(3)存在.满足条件的点P有两个.
①过点C作CP∥BD,交x轴于P,则∠PCB=∠CBD,
∵直线BD解析式为y=3x9,
∵直线CP过点C,
∴直线CP的解析式为y=3x3,
∴点P坐标(1,0),
②连接BD′,过点C作CP′∥BD′,交x轴于P′,
∴∠P′CB=∠D′BC,
根据对称性可知∠D′BC=∠CBD,
∴∠P′CB=∠CBD,
∵直线BD′的解析式为![]()
∵直线CP′过点C,
∴直线CP′解析式为![]() ,
,
∴P′坐标为(9,0),
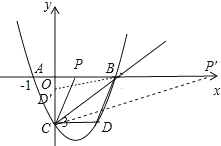
综上所述,满足条件的点P坐标为(1,0)或(9,0).

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案