题目内容
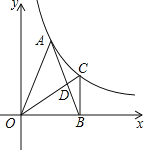
【题目】如图,AB是⊙O的弦,过点O作OC⊥OA,OC交于AB于P,且CP=CB.
(1)求证:BC是⊙O的切线;
(2)已知∠BAO=25°,点Q是弧AmB上的一点.
①求∠AQB的度数;
②若OA=18,求弧AmB的长.
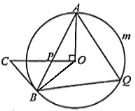
【答案】(1)见解析;(2)①∠AQB=65°,②l弧AmB=23π.
【解析】
(1)连接OB,根据等腰三角形的性质得到∠OAB=∠OBA,∠CPB=∠CBP,再根据∠PAO+∠APO=90°,继而得出∠OBC=90°,问题得证;
(2)①根据等腰三角形的性质可得∠ABO=25°,再根据三角形内角和定理可求得∠AOB的度数,继而根据圆周角定理即可求得答案;
②根据弧长公式进行计算即可得.
(1)连接OB,
∵CP=CB,
∴∠CPB=∠CBP,
∵OA⊥OC,
∴∠AOC=90°,
∵OA=OB,
∴∠OAB=∠OBA,
∵∠PAO+∠APO=90°,
∴∠ABO+∠CBP=90°,
∴∠OBC=90°,
∴BC是⊙O的切线;

(2)①∵∠BAO=25° ,OA=OB,
∴∠OBA=∠BAO=25°,
∴∠AOB=180°-∠BAO-∠OBA=130°,
∴∠AQB=![]() ∠AOB=65°;
∠AOB=65°;
②∵∠AOB=130°,OB=18,
∴l弧AmB=![]() =23π.
=23π.

练习册系列答案
相关题目