题目内容
【题目】（操作体验）
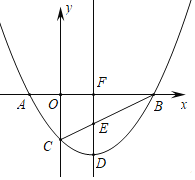
如图①，已知线段AB和直线l，用直尺和圆规在l上作出所有的点P，使得∠APB=30°，如图②，小明的作图方法如下：
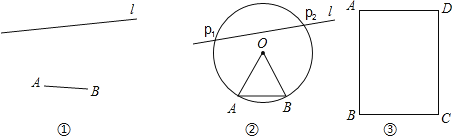
第一步：分别以点A，B为圆心，AB长为半径作弧，两弧在AB上方交于点O；
第二步：连接OA，OB；
第三步：以O为圆心，OA长为半径作⊙O，交l于P1，P2；所以图中P1，P2即为所求的点．
（1）在图②中，连接P1A，P1B，试说明∠AP1B=30°；
（方法迁移）
（2）已知矩形ABCD，如图③，BC=2
，AB=m．
①若P为AD边上的点，且满足∠BPC=60°的点P恰有1个，求m的值．
②当m=4时，若P为矩形ABCD外一点，且满足∠BPC=60°，求AP长的取值范围．
【答案】（1）说明见解析；（2）①m= 3；②AP长的取值范围为2＜AP＜4或4＜AP＜
．
【解析】
（1）由圆周角定理可知∠AP1B=
∠AOB=30°；
（2）①由题意可画出图形，当⊙O与AD相切且圆心角∠BOC=120°时，满足∠BPC=60°的点P恰有1个，此时可构造直角三角形，通过勾股定理，求出m的值；
②由题意可画出图形，当点P在弧BR和弧SC上（不含端点）运动时，满足∠BPC= ∠BOC=60°，分别求得AP长的范围即可得出答案．
解：（1）由作法，可得OA=OB=AB，
∴△OAB为等边三角形，
∴∠AP1B=∠AOB=30°；
（2）①如图1，在矩形内作∠BOC=120°，OB=OC，作直线OM⊥BC于M，交AD于P，
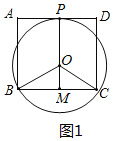
则PM⊥AD，∠BPC=∠BOC=60°
当⊙O与AD相切于点P时，满足∠BPC=60°的点P恰有1个，
∵BC=2
，AB=m．
∴OB=OC=2，
∵OM=BO=1，OP=OB=2，
∴m=OP+OM=2+1=3；
②如图2，设⊙O与AB，CD的另一个交点分别为R，S，
当点P在弧BR和弧SC上（不含端点）运动时，满足∠BPC=∠BOC=60°，
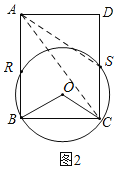
当P在弧BR上运动时，
P与R重合时，BR=
BC=2，AP=2，
P与B重合时，AP=4，
当P在弧SC上运动时，
P与S重合时，AP=
，
P与C重合时，AP=
，
∴当m=4时，P为矩形ABCD外一点，且满足∠BPC=60°，AP长的取值范围为2＜AP＜4或4＜AP＜．
故答案为：（1）说明见解析；（2）①m= 3；②AP长的取值范围为2＜AP＜4或4＜AP＜．
