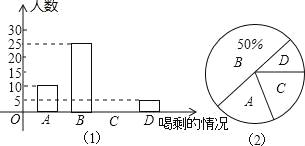
题目内容
【题目】如图:在直角三角形ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B,填写下列空格:
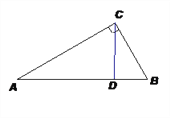
证明:∵∠ACB=90° (已知)
∴∠A+∠B=90° (______________)
∵∠ACD=∠B (已知)
∴∠A+∠ACD=90° (_______________)
∴△ACD是直角三角形 (_______________)
【答案】 直角三角形中两锐角互余, 等量代换, 有两角互余的三角形是直角三角形,
【解析】证明:∵∠ACB=90° (已知)
∴∠A+∠B=90° (直角三角形中两锐角互余)
∵∠ACD=∠B (已知)
∴∠A+∠ACD=90° (等量代换)
∴△ACD是直角三角形 (有两角互余的三角形是直角三角形)

练习册系列答案
相关题目