Question

【题目】在一个三角形中，若一条边等于另一条边的两倍，则称这种三角形为“倍边三角形”． 例如：边长为a=2，b=3，c=4的三角形就是一个倍边三角形．

（1）如果一个倍边三角形的两边长为6和8，那么第三条边长所有可能的值为 ．

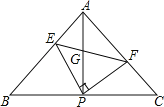
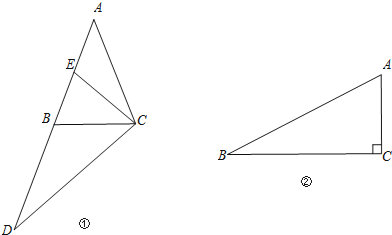
（2）如图①，在△ABC中，AB=AC，延长AB到D，使BD=AB，E是AB的中点．

求证：△DCE是倍边三角形；

（3）如图②，Rt△ABC中，∠C=90°，AC=4，BC=8，若点D在边AB上（点D不与A、B重合），且△BCD是倍边三角形，求BD的长．

Answer 1

【答案】（1）3，4，12；（2）见解析；（3）BD=4或或或．

【解析】

试题分析：（1）直接利用倍边三角形的定义求解即可求得答案，注意三角形的三边关系；

（2）由已知，易证得△ACD∽△AEC，然后由相似三角形的对应边成比例，证得CD=2CE，即可证得结论；

（3）分BC=2BD、BC=2CD、BD=2CD、CD=2BD四种情况进行解答，求出各种情况下BD的长．

（1）解：∵一个倍边三角形的两边长为6和8，

∴第三边可能为：3，4，12，16，

∵6+8＜16，不能组成三角形，舍去，

∴第三边可能为：3，4，12；

故答案为：3，4，12；

（2）证明：∵BD=AB=AC，

∴AD=2AC．即=2．

∵E是AB的中点，

∴AB=2AE．

∴AC=2AE．即=2，

∴=．

又∵∠A=∠A，

∴△ACD∽△AEC．

∴=2．

∴△DCE是倍边三角形．

（3）∵在Rt△ABC中，∠C=90°，AC=4，BC=8，

∴AB==4，

①当BC=2BD时，BD=4；

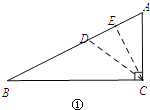
②当BC=2CD时，如图①，

CD=4，作CE⊥AB于E，

tanA===2，

设AE=x，则CE=2x，AC=x，

∴x=4．x=．

∴AE=，

在△ACD中，CD=AC=4，CE⊥AB，

∴AD=2AE=．

∴BD=AB﹣AD=；

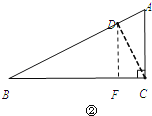
③当BD=2CD时，如图②，作DF⊥BC于F，

tanB===，

设DF=y，则BF=2y，BD=y，

∴CD=y，CF=y．

∵BC=BF+CF，

∴8=2y+y．

解得y=．

∴BD=；

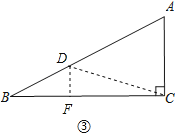
④当CD=2BD时，如图③，过点D作DF⊥BC于F，

tanB===，

设DF=z，则BF=2z，BD=z，

∴CD=2z，CF=z．

∵BC=BF+CF，

∴8=2z+z．

解得z=，

∴DF=，

∴BD=；

综上所述，BD=4或或或．