Question

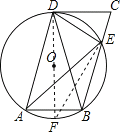
【题目】如图，在ABCD中，过A、B、D三点的⊙O交BC于点E，连接DE，∠CDE=∠DAE．

（1）求证：DE=DC；

（2）求证：直线DC是⊙O的切线．

Answer 1

【答案】见解析

【解析】

试题分析：（1）由平行四边形的性质得出AD∥BC，AB=DC，进而证得∠DAE=∠AEB，证出=，即可得出DE=DC；

（2）作直径DF，连接EF，则∠EFD=∠EAD，证出∠EFD=∠CDE，再由DF是⊙O的直径，得出∠DEF=90°，得出∠FDC=90°，即可得出结论．

（1）证明：∵四边形ABCD是平行四边形，

∴AD∥BC，AB=DC，

∴∠DAE=∠AEB．

∴=，

∴AB=DE，

∴DE=DC；

（2）解：如图所示：作直径DF，连接EF．

则∠EFD=∠EAD，

∵∠CDE=∠DAE，

∴∠EFD=∠CDE．

∵DF是⊙O的直径，

∴∠DEF=90°，

∴∠EFD+∠FDE=90°，

∴∠CDE+∠FDE=90°

∴∠FDC=90°．

∴直线DC是⊙O的切线．