Question

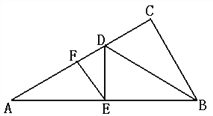
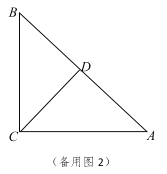
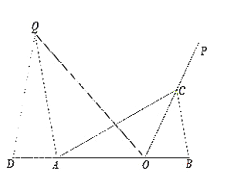
【题目】如图，点O在线段AB上，AO=2OB=2，，点C是射线OP上的一个动点．

（1）如图①，当，OC=2，求的值；

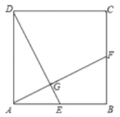
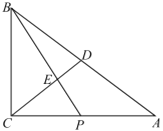
（2）如果②，当AC=AB时，求OC的长（用含的代数式表示）；

（3）在第（2）题的条件下，过点A作AQ//BC，并使，求的值．

Answer 1

【答案】（1）证明见解析；（2）；（3）

【解析】

（1）作CH⊥AB于H，构造三角形相似,根据三角形相似边对应关系即可解得a的值.

（2）作CH⊥AB于H，构造直角，根据勾股定理，即可用a表示出OC的长.

（3）在BA延长线上取一点D，使得QD＝QA，连接QD，根据,即可求得的值．

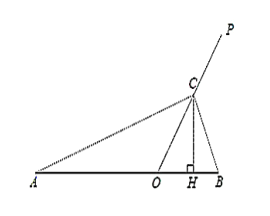
⑴ 过C作CH⊥AB于点H，

∵OC＝2，∠COH＝60°，

∴OH＝1，CH＝，

∴AH＝2a＋1，BH＝a－1，

∵∠ACB＝∠AHC＝90°，

△ACH∽△CBH，

∴CH2＝AH×HB，

∴3＝（2a＋1）（a－1），

a＝（a＝＜0，舍去）；

⑵ 过C作CH⊥AB于点H，

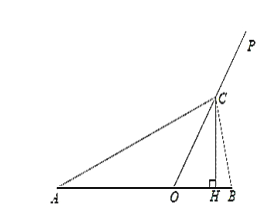
OH＝OC，CH＝OC，

∴AH＝2a＋OC，

AC＝AB＝3a，AC2＝AH2＋CH2，

∴，

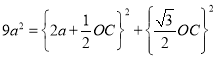＜0，舍去）；

（3）∠QAB＞90°，

在BA延长线上去一点D，使得QD＝QA，联接QD，∠QOC＝∠B，

∴∠QOD＝∠OCB，

∵∠D＝∠QAD＝∠B，

∴△QOD∽△OCB，

∴.

故答案为（1）a＝；（2）；（3）.