题目内容
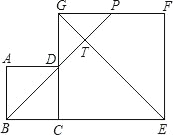
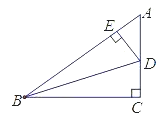
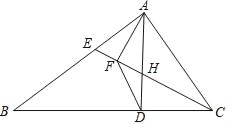
【题目】如图,在△ABC中,点D在边BC上,∠CAD=∠B,点E在边AB上,联结CE交AD于点H,点F在CE上,且满足CFCE=CDBC.
(1)求证:△ACF∽△ECA;
(2)当CE平分∠ACB时,求证:![]() =
=![]() .
.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据相似三角形的判定定理得到△ACD∽△BCA,求得![]() =
=![]() ,得到AC2=CDBC,等量代换得到AC2=CFCE,于是得到结论;
,得到AC2=CDBC,等量代换得到AC2=CFCE,于是得到结论;
(2)根据相似三角形的性质得到∠CAE=∠CDE,根据角平分线定义得到∠ACE=∠DCH,根据相似三角形的性质即可得到结论.
(1)∵∠ACD=∠BCA,∠CAD=∠B,
∴△ACD∽△BCA,
∴![]() =
=![]() ,
,
∴AC2=CDBC,
∵CFCE=CDBC,
∴AC2=CFCE,
∴![]() =
=![]() ,
,
∵∠ACF=∠ECA,
∴△ACF∽△ECA;
(2)∵△ACF∽△ECA,
∴∠CAE=∠CDE,
∵当CE平分∠ACB,
∴∠ACE=∠DCH,
∴△ACE∽△DCH,
∴![]() =
=![]() 2=
2=![]()
∵AC2=CDBC,
∴![]() =
=![]() .
.

【题目】被誉为“中原第一高楼”的郑州会展宾馆(俗称“大玉米”)坐落在风景如画的如意湖,是来郑州观光的游客留影的最佳景点.学完了三角函数知识后,刘明和王华同学决定用自己学到的知识测量“大王米”的高度,他们制订了测量方案,并利用课余时间完成了实地测量.测量项目及结果如下表:
项目 | 内容 | |||
课题 | 测量郑州会展宾馆的高度 | |||
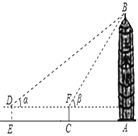
测量示意图 |
| 如图,在E点用测倾器DE测得楼顶B的仰角是α,前进一段距离到达C点用测倾器CF测得楼顶B的仰角是β,且点A、B、C、D、E、F均在同一竖直平面内 | ||
测量数据 | ∠α的度数 | ∠β的度数 | EC的长度 | 测倾器DE,CF的高度 |
40° | 45° | 53米 | 1.5米 | |
… | … | |||
请你帮助该小组根据上表中的测量数据,求出郑州会展宾馆的高度(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,结果保留整数)