题目内容
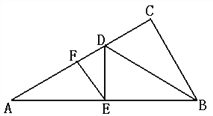
【题目】如图，在Rt△ABC中，∠C=90°，BD平分∠ABC，交AC于D，DE⊥AB于E,EF∥AC于F。
（1）求证：△EDF∽△ADE；
（2）猜想：线段DC、DF、DA之间存在什么关系？并说明理由。
【答案】（1）证明见解析；
（2）
,理由见解析.
【解析】（1）利用垂直的定义和平行线的性质可证明∠DFE=∠DEA=90°，则利用相似三角形的判定方法可判断△EDF∽△ADE；
（2）由于△EDF∽△ADE，则利用相似比可得到DE2=DE×DA，再利用角平分线的性质定理得到DE=DC，从而得到线段DC，DF、DA之间的关系.
（1）证明：∵EF//BC
∴∠EFD=∠C=90°
∵DE⊥AB，
∴∠DEA=∠EFD=90°
又∵∠EDF=∠ADE
∴
∽
（2）
∵∠C=∠DEB=90°，BD平分∠ABC
∴DE=DC
由（1）得∽
∴
∴
∴
“点睛”本题考查了相似三角形的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的一般方法是通过作平行线构造相似三角形，解决本题的关键是利用相似三角形比得到DE、DF、DA的关系.
练习册系列答案
名校课堂系列答案
相关题目
【题目】八（2）班组织了一次经典朗读比赛，甲、乙两队各10人的比赛成绩如表（10分制）：
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
（1）甲队成绩的中位数是分，乙队成绩的众数是分；
（2）计算甲、乙队的平均成绩和方差，试说明成绩较为整齐的是哪一队？
