Question

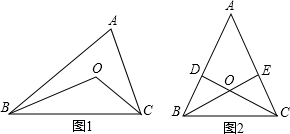
如图1，在△ABC中，OB、OC是∠ABC、∠ACB的角平分线；
（1）填写下面的表格．

∠A的度数	50°	60°	70°
∠BOC的度数

（2）试猜想∠A与∠BOC之间存在一个怎样的数量关系，并证明你的猜想；
（3）如图2，△ABC的高BE、CD交于O点，试说明图中∠A与∠BOD的关系．

Answer 1

分析：（1）由∠A=90°+

1

2

∠BOC，代入数值即可求得答案；
（2）由在△ABC中，OB、OC是∠ABC、∠ACB的角平分线，根据三角形的内角和定理即可求得∠OBC+∠OCB的值，然后在△OBC中，再利用三角形的内角和定理，即可求得答案；
（3）由△ABC的高BE、CD交于O点，即可得∠BDC=∠BEA=90°，然后利用同角的余角相等，即可求得∠A与∠BOD的关系．

解答：解：（1）

∠A的度数	50°	60°	70°
∠BOC的度数	115°	120°	125°

（2）猜想：∠BOC=90°+

1

2

∠A．
理由：∵在△ABC中，OB、OC是∠ABC、∠ACB的角平分线；
∴∠OBC=

1

2

∠ABC，∠OCB=

1

2

∠ACB，
∵∠ABC+∠ACB=180°-∠A，
∴∠OBC+∠OCB=

1

2

（∠ABC+∠ACB）=

1

2

（180°-∠A）=90°-

1

2

∠A，
∴∠BOC=180°-（∠OBC+∠OCB）=180°-（90°-

1

2

∠A）=90°+

1

2

∠A．

（3）证明：∵△ABC的高BE、CD交于O点，
∴∠BDC=∠BEA=90°，
∴∠ABE+∠BOD=90°，∠ABE+∠A=90°，
∴∠A=∠BOD．

点评：此题考查了三角形的内角和定理与同角的余角相等，以及角平分线的定义．此题难度适中，解题的关键是整体思想与数形结合思想的应用．