题目内容
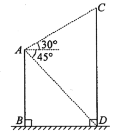
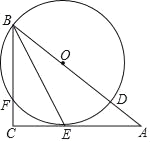
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F
(1)求证:AC是⊙O的切线;
(2)若CF=2,CE=4,求⊙O的半径.
【答案】(1)见解析;(2)⊙O的半径为5.
【解析】
(1)根据角平分线的定义和同圆的半径相等可得:OE∥BC,所以∠OEA=90°,则AC是⊙O的切线;
(2)过点O作OH⊥BF交BF于H,先求OH和BH的长,再根据勾股定理求OB的长.
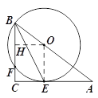
(1)证明:连接OE.
∵OE=OB,
∴∠OBE=∠OEB,
∵BE平分∠ABC,
∴∠OBE=∠EBC,
∴∠EBC=∠OEB,
∴OE∥BC,
∴∠OEA=∠C,
∵∠ACB=90°,
∴∠OEA=90°,
∴AC是⊙O的切线;
(2)解:设⊙O的半径为r.
过点O作OH⊥BF交BF于H,
由题意可知四边形OECH为矩形,
∴OH=CE=4,CH=OE=r,
∴BH=FH=CH-CF=r-2,
在Rt△BHO中,∵OH2+BH2=OB2,
∴42+(r-2)2=r2,
解得r=5.
∴⊙O的半径为5.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】甲、乙两名同学分别进行6次射击训练,训练成绩(单位:环)如下表
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六交 | |
甲 | 9 | 8 | 6 | 7 | 8 | 10 |
乙 | 8 | 7 | 9 | 7 | 8 | 8 |
对他们的训练成绩作如下分析,其中说法正确的是( )
A. 他们训练成绩的平均数相同 B. 他们训练成绩的中位数不同
C. 他们训练成绩的众数不同 D. 他们训练成绩的方差不同