Question

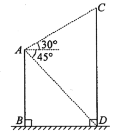
【题目】如图，在楼顶点处观察旗杆测得旗杆顶部的仰角为30°，旗杆底部的俯角为45°.已知楼高m，则旗杆的高度为___．（结果保留根号）

Answer 1

【答案】

【解析】

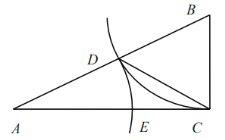
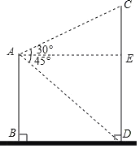
过点A作AE⊥CD于点E，由平行线的性质可知∠ADB＝∠EAD＝45°，故可得出AB＝BD＝9m，再根据正方形的判定定理得出四边形ABDE是正方形，故可得出AE＝BD，由锐角三角函数的定义求出CE的长，进而可得出结论．

解：如图，过点A作AE⊥CD于点E，

∵AE∥BD，

∴∠ADB＝∠EAD＝45°，

∴AB＝BD＝9m．

∵AB⊥BD，ED⊥BD，AE⊥CD，AB＝BD，

∴四边形ABDE是正方形，

∴AE＝BD＝AB＝DE＝9m．

在Rt△ACE中，

∵∠CAE＝30°，

∴CE＝AEtan30°＝9×＝3，

∴CD＝CE＋DE＝（3＋9）m．

故答案为：.