Question

【题目】 如图，在△DBC 中，DB＝DC，A 为△DBC 外一点，且∠BAC＝∠BDC，DM⊥AC 于 M．

（1）求证：AD 平分△ABC 的外角；

（2）判断 AM、AC、AB 有怎样的数量关系，并证明你的结论．

Answer 1

【答案】（1）见解析；（2）AC﹣AB＝2AM．

【解析】

1）如图 1 中，作 DN⊥BA 交 BA 的延长线于点 N．只要证明△DNB≌

△DMC（AAS），即可推出 DN＝DM 解决问题；

（2）结论：AC﹣AB＝2AM．利用全等三角形的性质即可证明；

（1）证明：如图 1 中，作 DN⊥BA 交 BA 的延长线于点 N．

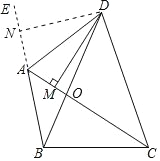
∵∠BAO＝∠ODC，∠AOB＝∠DOC，

∴∠ABO＝∠DCO，

∵DM⊥AC，DN⊥AB，

∴∠DNB＝∠DMC＝90°，

∵DB＝DC，

∴△DNB≌△DMC（AAS），

∴DN＝DM，∵DM⊥AC，DN⊥AB，

AD 平分△ABC 的外角；

（2）结论：AC﹣AB＝2AM．

理由：∵DN＝DM，DA＝DA，∠DNA＝∠DMA＝90°，

∴Rt△DNA≌Rt△DMA（HL），

∴AN＝AM，

∵△DNB≌△DMC（AAS），

∴BN＝CM，

∴AC﹣AB＝AM+CN﹣（BN﹣AN）＝2AM．