题目内容
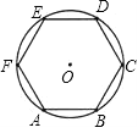
【题目】如图,已知![]() 的周长等于
的周长等于![]() ,则它的内接正六边形ABCDEF的面积是( )
,则它的内接正六边形ABCDEF的面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
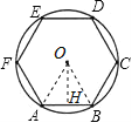
过点O作OH⊥AB于点H,连接OA,OB,由⊙O的周长等于6πcm,可得⊙O的半径,又由圆的内接多边形的性质可得∠AOB=60°,即可证明△AOB是等边三角形,根据等边三角形的性质可求出OH的长,根据S正六边形ABCDEF=6S△OAB即可得出答案.
过点O作OH⊥AB于点H,连接OA,OB,设⊙O的半径为r,
∵⊙O的周长等于6πcm,
∴2πr=6π,
解得:r=3,
∴⊙O的半径为3cm,即OA=3cm,
∵六边形ABCDEF是正六边形,
∴∠AOB=![]() ×360°=60°,OA=OB,
×360°=60°,OA=OB,
∴△OAB是等边三角形,
∴AB=OA=3cm,
∵OH⊥AB,
∴AH=![]() AB,
AB,
∴AB=OA=3cm,
∴AH=![]() cm,OH=
cm,OH=![]() =
=![]() cm,
cm,
∴S正六边形ABCDEF=6S△OAB=6×![]() ×3×
×3×![]() =
=![]() (cm2).
(cm2).
故选C.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目