题目内容
【题目】如图，二次函数图象过A，B，C三点，点A的坐标为（﹣1，0），点B的坐标为（4，0），点C在y轴正半轴上，且AB＝OC．
（1）求点C的坐标；
（2）求二次函数的解析式．
【答案】（1）C点的坐标为（0，5）；（2）y＝﹣
x2+
x+5．
【解析】
（1）先求出AB，再求出OC，即可得出C的坐标；
（2）把A、B、C的坐标代入函数解析式，即可求出a、b、c的值，即可得出答案．
解：（1）∵点A的坐标为（﹣1，0），点B的坐标为（4，0），
∴AB＝1+4＝5，
∵AB＝OC，
∴OC＝5，
∴C点的坐标为（0，5）；
（2）设过A、B、C点的二次函数的解析式为y＝ax2+bx+c，
把A、B、C的坐标代入得：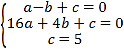
，
解得：a＝﹣，b＝，c＝5，
所以二次函数的解析式为y＝﹣x2+x+5．
练习册系列答案
相关题目
【题目】 郑州外国语中学为了解学生课下阅读所用时间的情况，从各年级学生中随机抽查了一部分学生进行统计，下面是针对此次统计所制作的不完整的频数分布表和频数分布直方图，请根据图表信息回答下列问题：
组别 | 时间段（小时） | 频数 | 频率 |
1 | 0≤x＜0.5 | 10 | 0.05 |
2 | 0.5≤x＜1.0 | 20 | 0.10 |
3 | 1.0≤x＜1.5 | 80 | b |
4 | 1.5≤x＜2.0 | a | 0.35 |
5 | 2.0≤x＜2.5 | 12 | 0.06 |
6 | 2.5≤x＜3.0 | 8 | 0.04 |
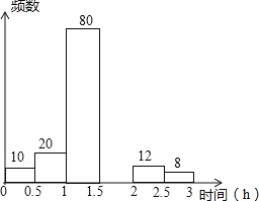
（1）表中a=______b=______；
（2）请补全频数分布直方图；
（3）样本中，学生日阅读所用时间的中位数落在第______组；
（4）该校共有学生3000人，请估计学生日阅读量不少于1.5小时的人数．
