ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣœΏΕΈAB=2Θ§MNΓΆAB”ΎΒψMΘ§«“AM=BMΘ§P «…δœΏMN…œ“ΜΕ·ΒψΘ§EΘ§DΖ÷±π «PAΘ§PBΒΡ÷–ΒψΘ§ΙΐΒψAΘ§MΘ§DΒΡ‘≤”κBPΒΡΝμ“ΜΫΜΒψCΘ®ΒψC‘ΎœΏΕΈBD…œΘ©Θ§Ν§ΫαACΘ§DEΘ°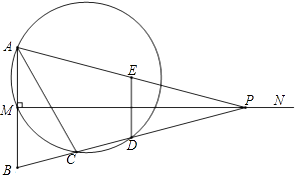
Θ®1Θ©Β±ΓœAPB=28Γψ ±Θ§«σΓœBΚΆ ![]() ΒΡΕ» ΐΘΜ
ΒΡΕ» ΐΘΜ
Θ®2Θ©«σ÷ΛΘΚAC=ABΘ°
Θ®3Θ©‘ΎΒψPΒΡ‘ΥΕ·Ιΐ≥Χ÷–
ΔΌΒ±MP=4 ±Θ§»ΓΥΡ±Ώ–ΈACDE“Μ±ΏΒΡΝΫΕΥΒψΚΆœΏΕΈMP…œ“ΜΒψQΘ§»τ“‘’β»ΐΒψΈΣΕΞΒψΒΡ»ΐΫ«–Έ «÷±Ϋ«»ΐΫ«–ΈΘ§«“QΈΣ»ώΫ«ΕΞΒψΘ§«σΥυ”–¬ζΉψΧθΦΰΒΡMQΒΡ÷ΒΘΜ
ΔΎΦ«AP”κ‘≤ΒΡΝμ“ΜΗωΫΜΒψΈΣFΘ§ΫΪΒψF»ΤΒψD–ΐΉΣ90ΓψΒΟΒΫΒψGΘ§Β±ΒψG«ΓΚΟ¬δ‘ΎMN…œ ±Θ§Ν§ΫαAGΘ§CGΘ§DGΘ§EGΘ§÷±Ϋ”–¥≥ωΓςACGΚΆΓςDEGΒΡΟφΜΐ÷°±»Θ°
ΓΨ¥πΑΗΓΩ
Θ®1Θ©
ΫβΘΚΓΏMNΓΆABΘ§AM=BMΘ§
ΓύPA=PBΘ§
ΓύΓœPAB=ΓœBΘ§
ΓΏΓœAPB=28ΓψΘ§
ΓύΓœB=76ΓψΘ§
»γΆΦ1Θ§Ν§Ϋ”MDΘ§

ΓΏMDΈΣΓςPABΒΡ÷–ΈΜœΏΘ§
ΓύMDΓΈAPΘ§
ΓύΓœMDB=ΓœAPB=28ΓψΘ§
Γύ ![]() =2ΓœMDB=56ΓψΘΜ
=2ΓœMDB=56ΓψΘΜ
Θ®2Θ©
÷ΛΟςΘΚΓΏΓœBAC=ΓœMDC=ΓœAPBΘ§
”÷ΓΏΓœBAP=180Γψ©¹ΓœAPB©¹ΓœBΘ§ΓœACB=180Γψ©¹ΓœBAC©¹ΓœBΘ§
ΓύΓœBAP=ΓœACBΘ§
ΓΏΓœBAP=ΓœBΘ§
ΓύΓœACB=ΓœBΘ§
ΓύAC=ABΘΜ
Θ®3Θ©
ΫβΘΚΔΌ»γΆΦ2Θ§Φ«MP”κ‘≤ΒΡΝμ“ΜΗωΫΜΒψΈΣRΘ§

ΓΏMD «RtΓςMBPΒΡ÷–œΏΘ§
ΓύDM=DPΘ§
ΓύΓœDPM=ΓœDMP=ΓœRCDΘ§
ΓύRC=RPΘ§
ΓΏΓœACR=ΓœAMR=90ΓψΘ§
ΓύAM2+MR2=AR2=AC2+CR2Θ§
Γύ12+MR2=22+PR2Θ§
Γύ12+Θ®4©¹PRΘ©2=22+PR2Θ§
ΓύPR= ![]() Θ§
Θ§
ΓύMR= ![]() Θ§
Θ§
ΔώΘ°Β±ΓœACQ=90Γψ ±Θ§AQΈΣ‘≤ΒΡ÷±ΨΕΘ§
ΓύQ”κR÷ΊΚœΘ§
ΓύMQ=MR= ![]() ΘΜ
ΘΜ
ΔρΘ°»γΆΦ3Θ§Β±ΓœQCD=90Γψ ±Θ§

‘ΎRtΓςQCP÷–Θ§PQ=2PR= ![]() Θ§
Θ§
ΓύMQ= ![]() ΘΜ
ΘΜ
ΔσΘ°»γΆΦ4Θ§Β±ΓœQDC=90Γψ ±Θ§

ΓΏBM=1Θ§MP=4Θ§
ΓύBP= ![]() Θ§
Θ§
ΓύDP= ![]() BP=
BP= ![]() Θ§
Θ§
ΓΏcosΓœMPB= ![]() =
= ![]() Θ§
Θ§
ΓύPQ= ![]() Θ§
Θ§
ΓύMQ= ![]() ΘΜ
ΘΜ
ΔτΘ°»γΆΦ5Θ§Β±ΓœAEQ=90Γψ ±Θ§

”…Ε‘≥Τ–‘Ω…ΒΟΓœAEQ=ΓœBDQ=90ΓψΘ§
ΓύMQ= ![]() ΘΜ
ΘΜ
Ήέ…œΥυ ωΘ§MQΒΡ÷ΒΈΣ ![]() Μρ
Μρ ![]() Μρ
Μρ ![]() ΘΜ
ΘΜ
ΔΎΓςACGΚΆΓςDEGΒΡΟφΜΐ÷°±»ΈΣ ![]() Θ°
Θ°
άμ”…ΘΚ»γΆΦ6Θ§ΓΏDMΓΈAFΘ§
ΓύDF=AM=DE=1Θ§
”÷”…Ε‘≥Τ–‘Ω…ΒΟGE=GDΘ§
ΓύΓςDEG «Β»±Ώ»ΐΫ«–ΈΘ§
ΓύΓœEDF=90Γψ©¹60Γψ=30ΓψΘ§
ΓύΓœDEF=75Γψ=ΓœMDEΘ§
ΓύΓœGDM=75Γψ©¹60Γψ=15ΓψΘ§
ΓύΓœGMD=ΓœPGD©¹ΓœGDM=15ΓψΘ§
ΓύGMD=ΓœGDMΘ§
ΓύGM=GD=1Θ§
ΙΐCΉςCHΓΆAB”ΎHΘ§

”…ΓœBAC=30ΓψΩ…ΒΟCH= ![]() AC=
AC= ![]() AB=1=MGȧAH=
AB=1=MGȧAH= ![]() ȧ
Θ§
ΓύCG=MH= ![]() ©¹1Θ§
©¹1Θ§
ΓύSΓςACG= ![]() CGΓΝCH=
CGΓΝCH= ![]() Θ§
Θ§
ΓΏSΓςDEG= ![]() Θ§
Θ§
ΓύSΓςACGΘΚSΓςDEG= ![]() Θ°
Θ°
ΓΨΫβΈωΓΩΘ®1Θ©ΗυΨί»ΐΫ«–ΈABP «Β»―ϋ»ΐΫ«–ΈΘ§Ω…ΒΟΓœBΒΡΕ» ΐΘ§‘ΌΝ§Ϋ”MDΘ§ΗυΨίMDΈΣΓςPABΒΡ÷–ΈΜœΏΘ§Ω…ΒΟΓœMDB=ΓœAPB=28ΓψΘ§ΫχΕχΒΟΒΫ ![]() =2ΓœMDB=56ΓψΘΜΘ®2Θ©ΗυΨίΓœBAP=ΓœACBΘ§ΓœBAP=ΓœBΘ§Φ¥Ω…ΒΟΒΫΓœACB=ΓœBΘ§ΫχΕχΒΟ≥ωAC=ABΘΜΘ®3Θ©ΔΌΦ«MP”κ‘≤ΒΡΝμ“ΜΗωΫΜΒψΈΣRΘ§ΗυΨίAM2+MR2=AR2=AC2+CR2 Θ§ Φ¥Ω…ΒΟΒΫPR=
=2ΓœMDB=56ΓψΘΜΘ®2Θ©ΗυΨίΓœBAP=ΓœACBΘ§ΓœBAP=ΓœBΘ§Φ¥Ω…ΒΟΒΫΓœACB=ΓœBΘ§ΫχΕχΒΟ≥ωAC=ABΘΜΘ®3Θ©ΔΌΦ«MP”κ‘≤ΒΡΝμ“ΜΗωΫΜΒψΈΣRΘ§ΗυΨίAM2+MR2=AR2=AC2+CR2 Θ§ Φ¥Ω…ΒΟΒΫPR= ![]() Θ§MR=
Θ§MR= ![]() Θ§‘ΌΗυΨίQΈΣ÷±Ϋ«»ΐΫ«–Έ»ώΫ«ΕΞΒψΘ§Ζ÷ΥΡ÷÷«ιΩωΫχ––Χ÷¬έΘΚΒ±ΓœACQ=90Γψ ±Θ§Β±ΓœQCD=90Γψ ±Θ§Β±ΓœQDC=90Γψ ±Θ§Β±ΓœAEQ=90Γψ ±Θ§Φ¥Ω…«σΒΟMQΒΡ÷ΒΈΣ
Θ§‘ΌΗυΨίQΈΣ÷±Ϋ«»ΐΫ«–Έ»ώΫ«ΕΞΒψΘ§Ζ÷ΥΡ÷÷«ιΩωΫχ––Χ÷¬έΘΚΒ±ΓœACQ=90Γψ ±Θ§Β±ΓœQCD=90Γψ ±Θ§Β±ΓœQDC=90Γψ ±Θ§Β±ΓœAEQ=90Γψ ±Θ§Φ¥Ω…«σΒΟMQΒΡ÷ΒΈΣ ![]() Μρ
Μρ ![]() Μρ
Μρ ![]() ΘΜΔΎœ»≈–Ε®ΓςDEG «Β»±Ώ»ΐΫ«–ΈΘ§‘ΌΗυΨίGMD=ΓœGDMΘ§ΒΟΒΫGM=GD=1Θ§ΙΐCΉςCHΓΆAB”ΎHΘ§”…ΓœBAC=30ΓψΩ…ΒΟCH=
ΘΜΔΎœ»≈–Ε®ΓςDEG «Β»±Ώ»ΐΫ«–ΈΘ§‘ΌΗυΨίGMD=ΓœGDMΘ§ΒΟΒΫGM=GD=1Θ§ΙΐCΉςCHΓΆAB”ΎHΘ§”…ΓœBAC=30ΓψΩ…ΒΟCH= ![]() AC=1=MGΘ§Φ¥Ω…ΒΟΒΫCG=MH=
AC=1=MGΘ§Φ¥Ω…ΒΟΒΫCG=MH= ![]() ©¹1Θ§ΫχΕχΒΟ≥ωSΓςACG=
©¹1Θ§ΫχΕχΒΟ≥ωSΓςACG= ![]() CGΓΝCH=
CGΓΝCH= ![]() Θ§‘ΌΗυΨίSΓςDEG=
Θ§‘ΌΗυΨίSΓςDEG= ![]() Θ§Φ¥Ω…ΒΟΒΫΓςACGΚΆΓςDEGΒΡΟφΜΐ÷°±»Θ°
Θ§Φ¥Ω…ΒΟΒΫΓςACGΚΆΓςDEGΒΡΟφΜΐ÷°±»Θ°

ΓΨΧβΡΩΓΩΈΣΝΥΗϋΚΟΗΡ…ΤΚ”ΝςΒΡΥ°÷ Θ§÷ΈΈέΙΪΥΨΨωΕ®ΙΚ¬ρ10Χ®ΈέΥ°¥Πάμ…η±Η![]() œ÷”–AΘ§BΝΫ÷÷–ΆΚ≈ΒΡ…η±ΗΘ§Τδ÷–ΟΩΧ®ΒΡΦέΗώΘ§‘¬¥ΠάμΈέΥ°ΝΩ»γœ¬±μΘΚΨ≠Βς≤ιΘΚΙΚ¬ρ“ΜΧ®A–Ά…η±Η±»ΙΚ¬ρ“ΜΧ®B–Ά…η±ΗΕύ2Άρ‘ΣΘ§ΙΚ¬ρ2Χ®A–Ά…η±Η±»ΙΚ¬ρ3Χ®B–Ά…η±Η…Ό6Άρ‘ΣΘ°
œ÷”–AΘ§BΝΫ÷÷–ΆΚ≈ΒΡ…η±ΗΘ§Τδ÷–ΟΩΧ®ΒΡΦέΗώΘ§‘¬¥ΠάμΈέΥ°ΝΩ»γœ¬±μΘΚΨ≠Βς≤ιΘΚΙΚ¬ρ“ΜΧ®A–Ά…η±Η±»ΙΚ¬ρ“ΜΧ®B–Ά…η±ΗΕύ2Άρ‘ΣΘ§ΙΚ¬ρ2Χ®A–Ά…η±Η±»ΙΚ¬ρ3Χ®B–Ά…η±Η…Ό6Άρ‘ΣΘ°
A–Ά | B–Ά | |
ΦέΗώ | a | b |
¥ΠάμΈέΥ°ΝΩ | 240 | 200 |
![]() «σaΘ§bΒΡ÷ΒΘΜ
«σaΘ§bΒΡ÷ΒΘΜ
![]() ÷ΈΈέΙΪΥΨΨ≠‘ΛΥψΙΚ¬ρΈέΥ°¥Πάμ…η±ΗΒΡΉ Ϋπ≤Μ≥§Ιΐ105Άρ‘ΣΘ§Ρψ»œΈΣΗΟΙΪΥΨ”–ΡΡΦΗ÷÷ΙΚ¬ρΖΫΑΗΘΜ
÷ΈΈέΙΪΥΨΨ≠‘ΛΥψΙΚ¬ρΈέΥ°¥Πάμ…η±ΗΒΡΉ Ϋπ≤Μ≥§Ιΐ105Άρ‘ΣΘ§Ρψ»œΈΣΗΟΙΪΥΨ”–ΡΡΦΗ÷÷ΙΚ¬ρΖΫΑΗΘΜ
![]() ‘Ύ
‘Ύ![]() ΒΡΧθΦΰœ¬Θ§»τΟΩ‘¬“Σ«σ¥ΠάμΈέΥ°ΝΩ≤ΜΒΆ”Ύ2040Ε÷Θ§ΈΣΝΥΫΎ‘ΦΉ ΫπΘ§«κΡψΈΣ÷ΈΈέΙΪΥΨ…ηΦΤ“Μ÷÷Ήν Γ«°ΒΡΙΚ¬ρΖΫΑΗΘ°
ΒΡΧθΦΰœ¬Θ§»τΟΩ‘¬“Σ«σ¥ΠάμΈέΥ°ΝΩ≤ΜΒΆ”Ύ2040Ε÷Θ§ΈΣΝΥΫΎ‘ΦΉ ΫπΘ§«κΡψΈΣ÷ΈΈέΙΪΥΨ…ηΦΤ“Μ÷÷Ήν Γ«°ΒΡΙΚ¬ρΖΫΑΗΘ°