题目内容
【题目】公元前5世纪，毕达哥拉斯学派中的一名成员希伯索斯发现了无理数 
，导致了第一次数学危机， 是无理数的证明如下： 假设 是有理数，那么它可以表示成 
（p与q是互质的两个正整数）．于是（ ）2=（ ）2=2，所以，q2=2p2 ． 于是q2是偶数，进而q是偶数，从而可设q=2m，所以（2m）2=2p2 ， p2=2m2 ， 于是可得p也是偶数．这与“p与q是互质的两个正整数”矛盾．从而可知“ 是有理数”的假设不成立，所以， 是无理数．
这种证明“ 是无理数”的方法是（ ）
A.综合法
B.反证法
C.举反例法
D.数学归纳法
【答案】B
【解析】解：由题意可得：这种证明“ 
是无理数”的方法是反证法． 故选：B．
【考点精析】通过灵活运用反证法，掌握先假设命题中的结论不成立，然后由此经过推理，引出矛盾，判定所做的假设不正确，从而得到原命题成立，这种证明方法叫做反证法即可以解答此题．
练习册系列答案
相关题目
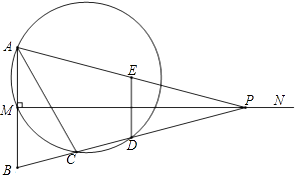
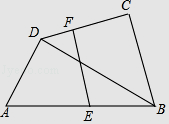
【题目】如图，AD是等腰△ABC底边BC上的高．点O是AC中点，延长DO到E，使OE=OD，连接AE，CE．
（1）求证：四边形ADCE的是矩形；
（2）若AB=17，BC=16，求四边形ADCE的面积．
【题目】体育委员统计了全班同学60秒跳绳的次数，并列出下面的频数分布表：
次数 | 60≤x＜90 | 90≤x＜120 | 120≤x＜150 | 150≤x＜180 | 180≤x＜210 |
频数 | 16 | 25 | 9 | 7 | 3 |
（1）全班有多少同学？
（2）组距是多少？组数是多少？
（3）跳绳次数x在120≤x＜180范围的同学有多少？占全班同学的百分之几（精确到0.1%）？
